Download this example as Jupyter notebook or Julia script.

5. Monte Carlo sampling of the Ising model

This tutorial illustrates simulation of the classical 2D Ising model.

using Sunny, GLMakie

Sunny expects a 3D Crystal unit cell. To model a square lattice, we create an orthogonal unit cell where the $z$-spacing is distinct from the $x$ and $y$ spacing.

a = 1
latvecs = lattice_vectors(a,a,10a,90,90,90)
crystal = Crystal(latvecs, [[0,0,0]])

Crystal
Spacegroup 'P 4/m m m' (123)
Lattice params a=1, b=1, c=10, α=90°, β=90°, γ=90°
Cell volume 10
Wyckoff 1a (point group '4/mmm'):
   1. [0, 0, 0]

Create a System of spins with linear size L in the $x$ and $y$ directions, and only one layer in the $z$ direction. The option :dipole means that the system will store Heisenberg spins, as opposed to SU($N$) coherent states. Polarize the initial spin configuration using polarize_spins!. Following the Ising convention, we will restrict these spins to the $z$-axis and give them magnitude $S=1$.

By default, Sunny expects the magnetic field in tesla. Selecting Units.theory instead allows for dimensionless units. Following Ising conventions, select $g=-1$ so that the Zeeman coupling between external field $𝐁$ and spin dipole $𝐬$ is $-𝐁⋅𝐬$.

L = 128
sys = System(crystal, (L,L,1), [SpinInfo(1, S=1, g=-1)], :dipole, seed=0)
polarize_spins!(sys, (0,0,1))

Use set_exchange! to include a ferromagnetic Heisenberg interaction along nearest-neighbor bonds. The Bond below connects two spins displaced by one lattice constant in the $x$-direction. This interaction will be propagated to all nearest-neighbors bonds in the system, consistent with the symmetries of the square lattice.

set_exchange!(sys, -1.0, Bond(1,1,(1,0,0)))

If an external field is desired, it can be set using set_field!.

B = 0
set_field!(sys, (0, 0, B))

The critical temperature for the Ising model is known analytically.

Tc = 2/log(1+√2)

2.269185314213022

Use a LocalSampler to perform nsweeps Monte Carlo sweeps. A sweep consists of, on average, one trial update per spin in the system. Each proposed update is accepted or rejected according to the Metropolis acceptance probability. As its name suggests, the propose_flip function will only propose pure spin flips, $𝐬 \rightarrow -𝐬$.

nsweeps = 4000
sampler = LocalSampler(kT=Tc, propose=propose_flip)
for i in 1:nsweeps
    step!(sys, sampler)
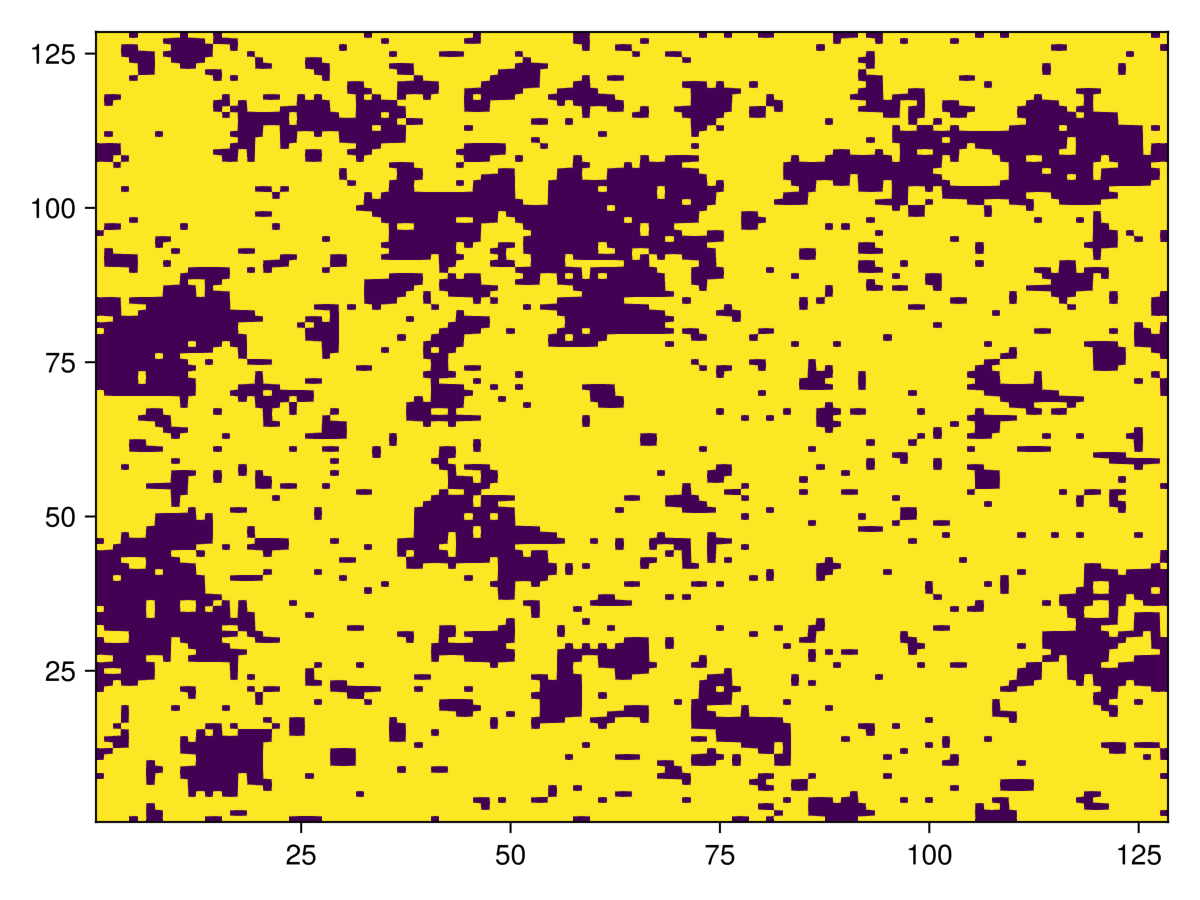
end

Plot the Ising spins by extracting the $z$-component of the dipoles

heatmap(reshape([s.z for s in sys.dipoles], (L,L)))