GitHub

Download this example as Jupyter notebook or Julia script.

SW15 - Ba₃NbFe₃Si₂O₁₄

This is a Sunny port of SpinW Tutorial 15, originally authored by Sandor Toth. The goal is to calculate the linear spin wave theory spectrum for Ba₃NbFe₃Si₂O₁₄.

Load packages

using Sunny, GLMakie

Build a Crystal for Ba₃NbFe₃Si₂O₁₄ using the crystal structure from Marty et al., Phys. Rev. Lett. 101, 247201 (2008).

a = b = 8.539 # (Å)
c = 5.2414
latvecs = lattice_vectors(a, b, c, 90, 90, 120)
types = ["Fe", "Nb", "Ba", "Si", "O", "O", "O"]
positions = [[0.24964,0,0.5], [0,0,0], [0.56598,0,0], [2/3,1/3,0.5220],
             [2/3,1/3,0.2162], [0.5259,0.7024,0.3536], [0.7840,0.9002,0.7760]]
langasite = Crystal(latvecs, positions, 150; types)
cryst = subcrystal(langasite, "Fe")
view_crystal(cryst)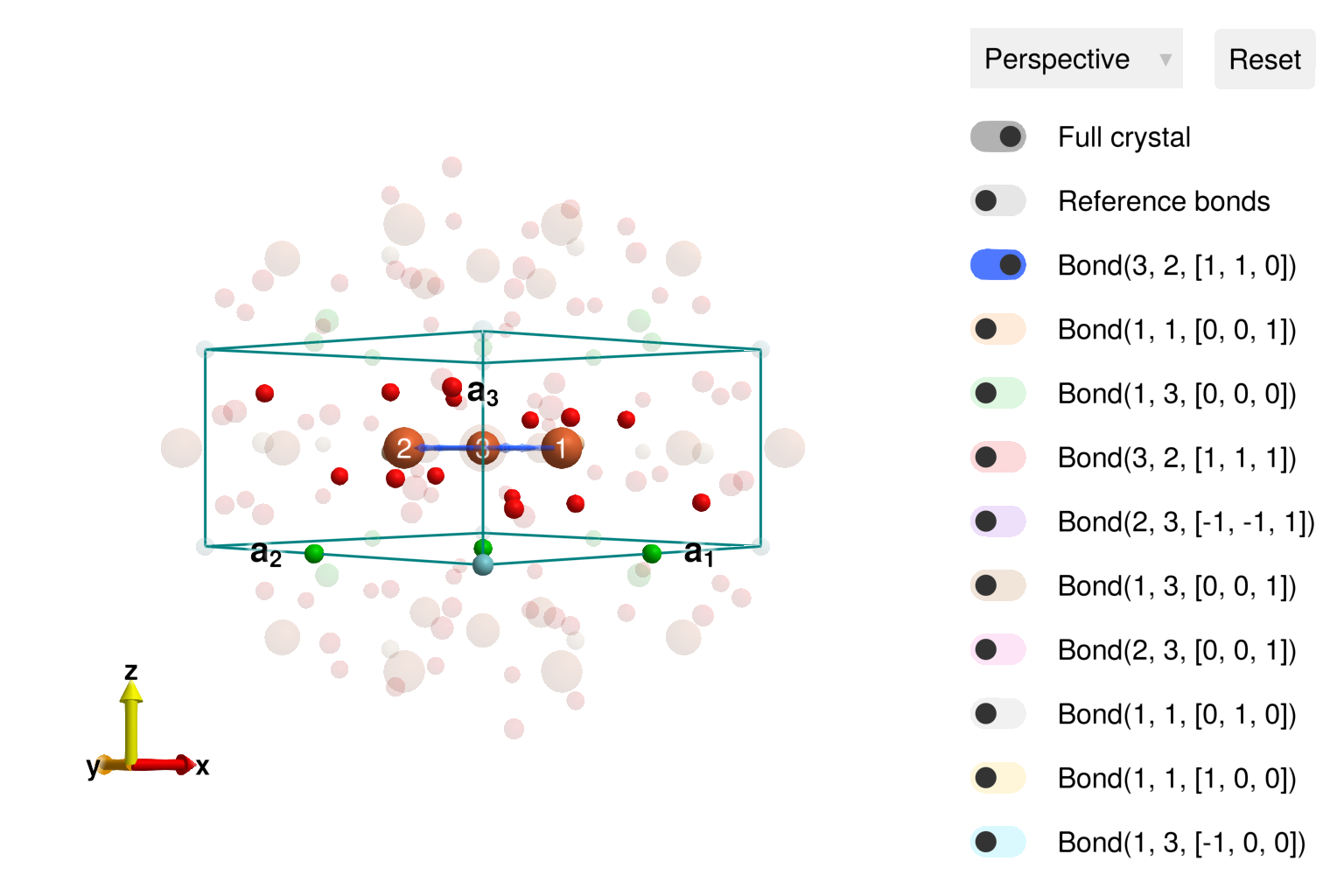
Example block output

Create a System with a lattice size of $(1,1,7)$. The magnetic structure of Ba₃NbFe₃Si₂O₁₄ was determined to have the ordering wavevector $𝐐=(0,0,1/7)$ and hence the magnetic unit cell has 7 sites.

latsize = (1,1,7)
S = 5/2
seed = 5
sys = System(cryst, latsize, [SpinInfo(1; S, g=2)], :dipole)
System [Dipole mode]
Lattice (1×1×7)×3
Energy per site 0

Set exchange interactions as parametrized in Loire et al., Phys. Rev. Lett. 106, 207201 (2011)

J₁ = 0.85
J₂ = 0.24
J₃ = 0.053
J₄ = 0.017
J₅ = 0.24
set_exchange!(sys, J₁, Bond(3, 2, [1,1,0]))
set_exchange!(sys, J₄, Bond(1, 1, [0,0,1]))
set_exchange!(sys, J₂, Bond(1, 3, [0,0,0]))

The final two exchanges define the chirality of the magnetic structure. The crystal chirality, $\epsilon_T$, the chirality of each triangle, $ϵ_D$ and the sense of rotation of the spin helices along $c$, $ϵ_{H}$. The three chiralities are related by $ϵ_T=ϵ_D ϵ_H$. We now assign $J_3$ and $J_5$ according to the crystal chirality.

ϵD = -1
ϵH = +1
ϵT = ϵD * ϵH

if ϵT == -1
    set_exchange!(sys, J₃, Bond(2, 3, [-1,-1,1]))
    set_exchange!(sys, J₅, Bond(3, 2, [1,1,1]))
elseif ϵT == 1
    set_exchange!(sys, J₅, Bond(2, 3, [-1,-1,1]))
    set_exchange!(sys, J₃, Bond(3, 2, [1,1,1]))
else
    throw("Provide a valid chirality")
end

Whilst Sunny provides tools to optimize the ground state automatically, in this case we already know the model ground state. Set the spiral magnetic order using set_spiral_order_on_sublattice!. It takes an ordering wavevector q, an axis of rotation for the spins axis, and the initial spin S0 for each sublattice.

k = [0, 0, 1/7]
axis = [0,0,1]
set_spiral_order_on_sublattice!(sys, 1; k, axis, S0=[1, 0, 0])
set_spiral_order_on_sublattice!(sys, 2; k, axis, S0=[-1/2, -sqrt(3)/2, 0])
set_spiral_order_on_sublattice!(sys, 3; k, axis, S0=[-1/2, +sqrt(3)/2, 0])

plot_spins(sys; color=[s[1] for s in sys.dipoles])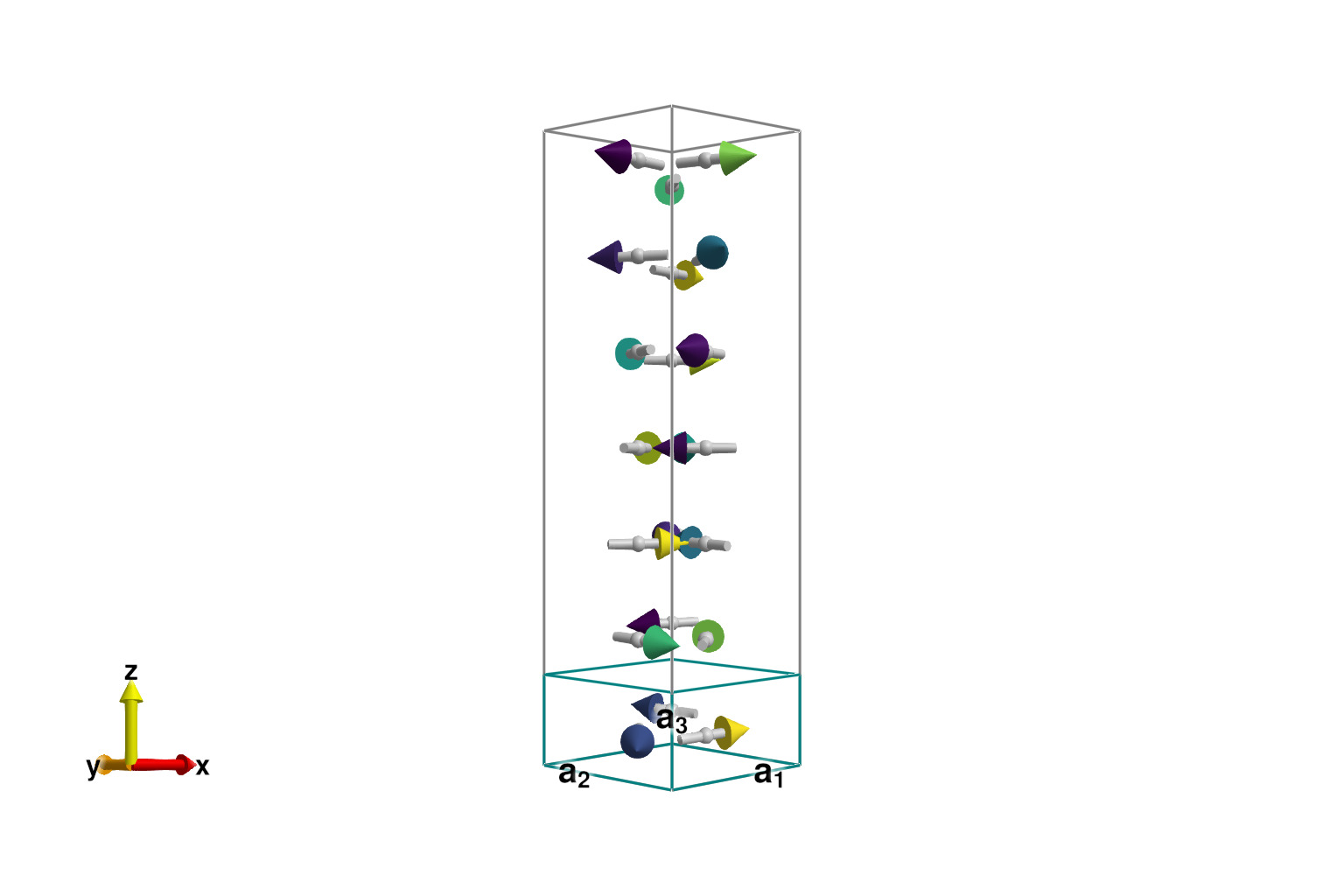
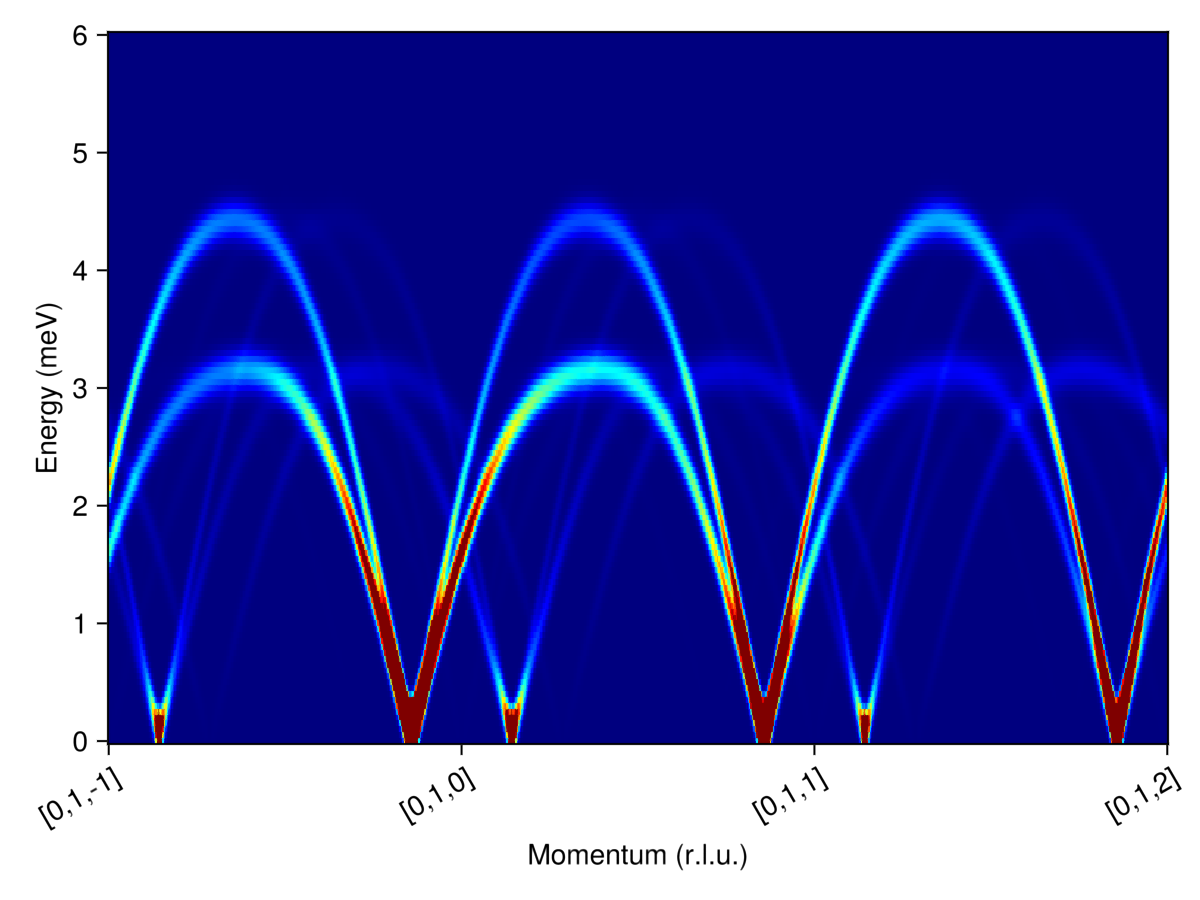
Example block output

Define a path in reciprocal space, $[0,1,-1+\xi]$ for $\xi = 0 \dots 3$.

points_rlu = [[0,1,-1],[0,1,-1+1],[0,1,-1+2],[0,1,-1+3]];
density = 200
path, xticks = reciprocal_space_path(cryst, points_rlu, density);

Calculate broadened intensities

swt = SpinWaveTheory(sys; energy_ϵ=1e-6)
broadened_formula = intensity_formula(swt, :perp; kernel=gaussian(fwhm=0.25))
energies = collect(0:0.05:6)  # 0 < ω < 6 (meV)
is = intensities_broadened(swt, path, energies, broadened_formula);

Plot

fig = Figure()
ax = Axis(fig[1,1]; xlabel="Momentum (r.l.u.)", ylabel="Energy (meV)",
          xticks, xticklabelrotation=π/6)
heatmap!(ax, 1:size(is,1), energies, is, colormap=:jet, colorrange=(0,150))
fig
Example block output