Download this example as Julia file or Jupyter notebook.
3. Multi-flavor spin wave simulations of FeI₂
This tutorial illustrates various advanced features such as symmetry analysis, energy minimization, and spin wave theory with multi-flavor bosons.
Our context will be FeI₂, an effective spin-1 material with strong single-ion anisotropy. Quadrupolar fluctuations give rise to a single-ion bound state that is observable in neutron scattering, and cannot be described by a dipole-only model. We will use the linear spin wave theory of SU(3) coherent states (i.e. 2-flavor bosons) to model the magnetic spectrum of FeI₂. The original study was performed in Bai et al., Nature Physics 17, 467–472 (2021).
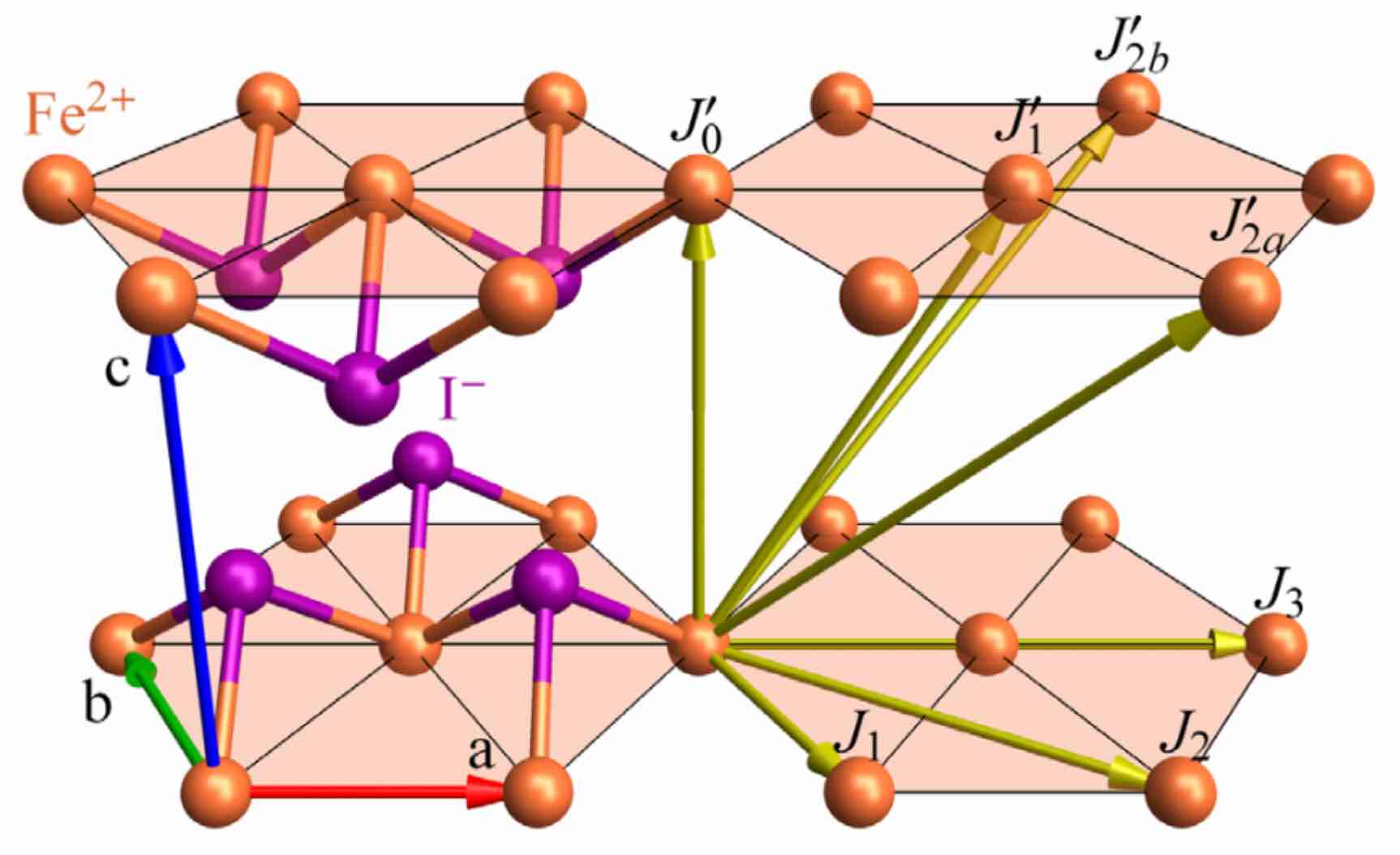
The Fe atoms are arranged in stacked triangular layers. The effective spin Hamiltonian takes the form,
\[\mathcal{H}=\sum_{(i,j)} 𝐒_i ⋅ J_{ij} 𝐒_j - D\sum_i \left(S_i^z\right)^2,\]
where the exchange matrices $J_{ij}$ between bonded sites $(i,j)$ include competing ferromagnetic and antiferromagnetic interactions. This model also includes a strong easy axis anisotropy, $D > 0$.
Load packages.
using Sunny, GLMakieConstruct the chemical cell of FeI₂ by specifying the lattice vectors and the full set of atoms.
units = Units(:meV, :angstrom)
a = b = 4.05012 # Lattice constants for triangular lattice (Å)
c = 6.75214 # Spacing between layers (Å)
latvecs = lattice_vectors(a, b, c, 90, 90, 120)
positions = [[0, 0, 0], [1/3, 2/3, 1/4], [2/3, 1/3, 3/4]]
types = ["Fe", "I", "I"]
cryst = Crystal(latvecs, positions; types)Crystal
Spacegroup 'P -3 m 1' (164)
Lattice params a=4.05, b=4.05, c=6.752, α=90°, β=90°, γ=120°
Cell volume 95.92
Type 'Fe', Wyckoff 1a (site sym. '-3m.'):
1. [0, 0, 0]
Type 'I', Wyckoff 2d (site sym. '3m.'):
2. [1/3, 2/3, 1/4]
3. [2/3, 1/3, 3/4]
Observe that the space group 'P -3 m 1' (164) has been inferred, as well as point group symmetries. Only the Fe atoms are magnetic, so we focus on them with subcrystal. Importantly, the new crystal retains the symmetry information for spacegroup 164.
cryst = subcrystal(cryst, "Fe")
view_crystal(cryst)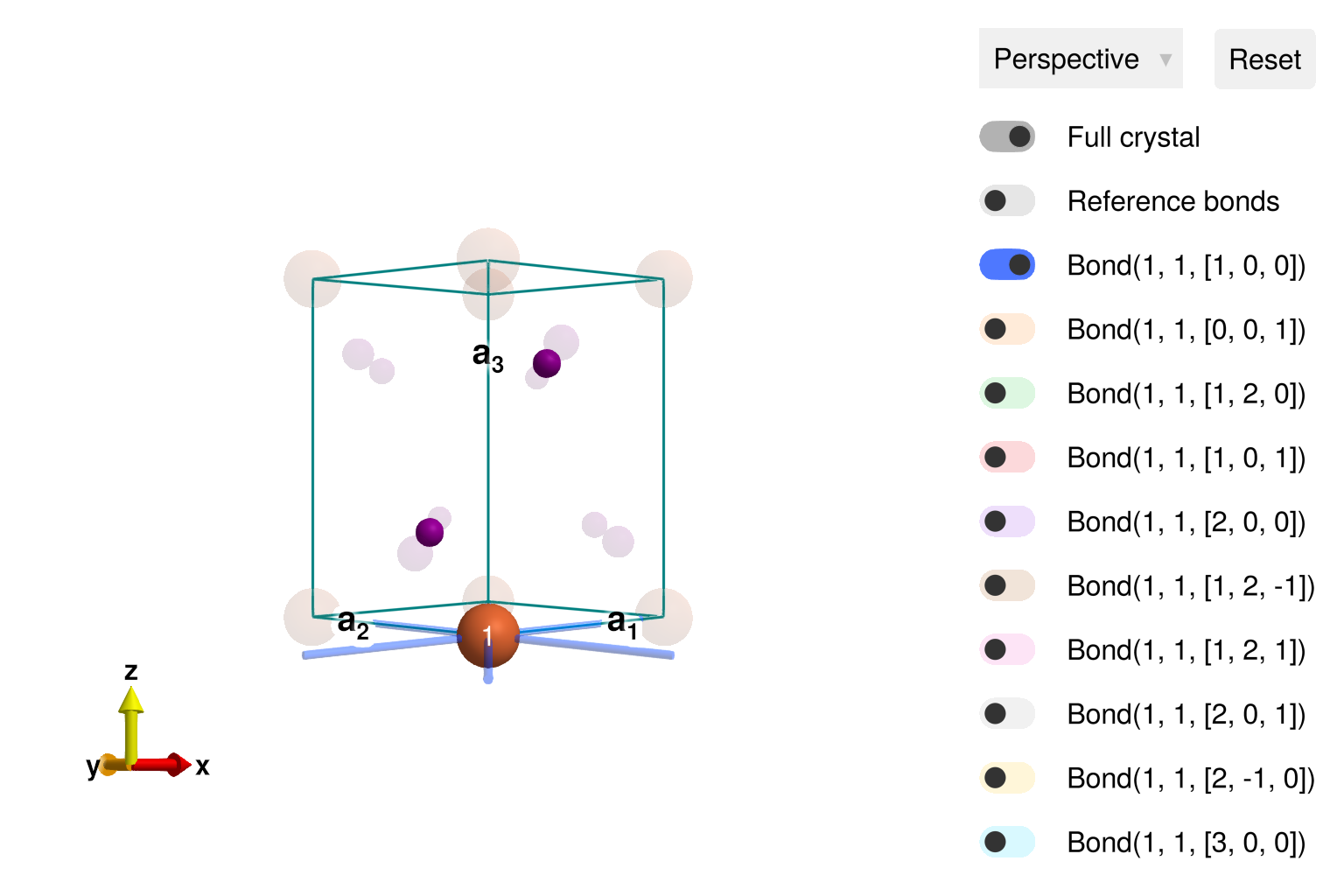
Symmetry analysis
The command print_symmetry_table provides a list of all the symmetry-allowed interactions out to 8 Å.
print_symmetry_table(cryst, 8.0)Atom 1
Type 'Fe', position [0, 0, 0], Wyckoff 1a
Allowed g-tensor: [A 0 0
0 A 0
0 0 B]
Allowed anisotropy in Stevens operators:
c₁*𝒪[2,0] +
c₂*𝒪[4,-3] + c₃*𝒪[4,0] +
c₄*𝒪[6,-3] + c₅*𝒪[6,0] + c₆*𝒪[6,6]
Bond(1, 1, [1, 0, 0])
Distance 4.05012, coordination 6
Connects 'Fe' at [0, 0, 0] to 'Fe' at [1, 0, 0]
Allowed exchange matrix: [A 0 0
0 B D
0 D C]
Bond(1, 1, [0, 0, 1])
Distance 6.75214, coordination 2
Connects 'Fe' at [0, 0, 0] to 'Fe' at [0, 0, 1]
Allowed exchange matrix: [A 0 0
0 A 0
0 0 B]
Bond(1, 1, [1, 2, 0])
Distance 7.015013617, coordination 6
Connects 'Fe' at [0, 0, 0] to 'Fe' at [1, 2, 0]
Allowed exchange matrix: [A 0 0
0 B D
0 D C]
Bond(1, 1, [1, 0, 1])
Distance 7.873681896, coordination 12
Connects 'Fe' at [0, 0, 0] to 'Fe' at [1, 0, 1]
Allowed exchange matrix: [A F E
F B D
E D C]The allowed $g$-tensor is expressed as a 3×3 matrix in the free coefficients A, B, ... The allowed single-ion anisotropy is expressed as a linear combination of Stevens operators. The latter correspond to polynomials of the spin operators, as we will describe below.
The allowed exchange interactions are given as 3×3 matrices for representative bonds. The notation Bond(i, j, n) indicates a bond between atom indices i and j, with cell offset n. Note that the order of the pair $(i, j)$ is significant if the exchange tensor contains antisymmetric Dzyaloshinskii–Moriya (DM) interactions.
The bonds can be visualized in the view_crystal interface. By default, Bond(1, 1, [1,0,0]) is toggled on, to show the 6 nearest-neighbor Fe-Fe bonds on a triangular lattice layer. Toggling Bond(1, 1, [0,0,1]) shows the Fe-Fe bond between layers, etc.
Defining the spin model
Construct a System with spin $s=1$ and $g=2$ for the Fe ions.
Recall that quantum spin-1 is, in reality, a linear combination of basis states $|m⟩$ with well-defined angular momentum $m = -1, 0, 1$. FeI₂ has a strong easy-axis anisotropy, which stabilizes a single-ion bound state of zero angular momentum, $|m=0⟩$. Such a bound state is inaccessible to traditional spin wave theory, which works with dipole expectation values of fixed magnitude. This physics is, however, well captured with a theory of SU(N) coherent states, where $N = 2S+1 = 3$ is the number of levels. Activate this generalized theory by selecting :SUN mode instead of :dipole mode.
An optional seed for random number generation can be used to to make the calculation exactly reproducible.
sys = System(cryst, [1 => Moment(s=1, g=2)], :SUN; seed=2)System [SU(3)]
Supercell (1×1×1)×1
Energy per site 0
Set the exchange interactions for FeI₂ following the fits of Bai et al.
J1pm = -0.236 # (meV)
J1pmpm = -0.161
J1zpm = -0.261
J2pm = 0.026
J3pm = 0.166
J′0pm = 0.037
J′1pm = 0.013
J′2apm = 0.068
J1zz = -0.236
J2zz = 0.113
J3zz = 0.211
J′0zz = -0.036
J′1zz = 0.051
J′2azz = 0.073
J1xx = J1pm + J1pmpm
J1yy = J1pm - J1pmpm
J1yz = J1zpm
set_exchange!(sys, [J1xx 0.0 0.0;
0.0 J1yy J1yz;
0.0 J1yz J1zz], Bond(1,1,[1,0,0]))
set_exchange!(sys, [J2pm 0.0 0.0;
0.0 J2pm 0.0;
0.0 0.0 J2zz], Bond(1,1,[1,2,0]))
set_exchange!(sys, [J3pm 0.0 0.0;
0.0 J3pm 0.0;
0.0 0.0 J3zz], Bond(1,1,[2,0,0]))
set_exchange!(sys, [J′0pm 0.0 0.0;
0.0 J′0pm 0.0;
0.0 0.0 J′0zz], Bond(1,1,[0,0,1]))
set_exchange!(sys, [J′1pm 0.0 0.0;
0.0 J′1pm 0.0;
0.0 0.0 J′1zz], Bond(1,1,[1,0,1]))
set_exchange!(sys, [J′2apm 0.0 0.0;
0.0 J′2apm 0.0;
0.0 0.0 J′2azz], Bond(1,1,[1,2,1]))The function set_onsite_coupling! assigns a single-ion anisotropy. The argument can be constructed using spin_matrices or stevens_matrices. Here we use Julia's anonymous function syntax to assign an easy-axis anisotropy along the direction $\hat{z}$.
D = 2.165 # (meV)
set_onsite_coupling!(sys, S -> -D*S[3]^2, 1)Finding the ground state
This model has been fitted so that energy minimization yields the physically correct ground state. Knowing this, we could set the magnetic configuration manually by calling set_dipole! on each site in the system. Another approach, as we will demonstrate, is to search for the ground-state via minimize_energy!.
To reduce bias in the search, use resize_supercell to create a relatively large system of 4×4×4 chemical cells. Randomize all spins (represented as SU(3) coherent states) and minimize the energy.
sys = resize_supercell(sys, (4, 4, 4))
randomize_spins!(sys)
minimize_energy!(sys)65The positive step-count above indicates successful convergence to a local energy minimum. Defects, however, are visually apparent.
plot_spins(sys; color=[S[3] for S in sys.dipoles])
One could precisely quantify the Fourier-space static structure factor $\mathcal{S}(𝐪)$ of this spin configuration using SampledCorrelationsStatic. For the present purposes, however, it is most convenient to use print_wrapped_intensities, which effectively averages $\mathcal{S}(𝐪)$ over all Brillouin zones.
print_wrapped_intensities(sys)Dominant wavevectors for spin sublattices:
[-1/4, 1/4, 1/4] 37.33% weight
[1/4, -1/4, -1/4] 37.33%
[-1/4, 1/4, 0] 1.60%
[1/4, -1/4, 0] 1.60%
[-1/4, 1/4, 1/2] 1.60%
[1/4, -1/4, 1/2] 1.60%
[1/4, -1/4, 1/4] 1.59%
[-1/4, 1/4, -1/4] 1.59%
[0, -1/4, 1/4] 0.77%
[0, 1/4, -1/4] 0.77%
[1/4, 0, 1/4] 0.77%
... ...The known zero-field energy-minimizing magnetic structure of FeI₂ is a two-up, two-down order. It can be described as a generalized spiral with a single propagation wavevector $𝐤$. Rotational symmetry allows for three equivalent orientations: $±𝐤 = [0, -1/4, 1/4]$, $[1/4, 0, 1/4]$, or $[-1/4,1/4,1/4]$. Energy minimization of large systems can easily get trapped in a metastable state with competing domains and defects. Nonetheless, print_wrapped_intensities shows that a non-trivial fraction of the total intensity is consistent with known ordering wavevectors.
Let's break the three-fold symmetry by hand. The function suggest_magnetic_supercell takes any number of $𝐤$ modes and suggests a magnetic cell shape that is commensurate with all of them.
suggest_magnetic_supercell([[0, -1/4, 1/4]])Possible magnetic supercell in multiples of lattice vectors:
[1 0 0; 0 2 1; 0 -2 1]
for the rationalized wavevectors:
[[0, -1/4, 1/4]]Using the minimal system returned by reshape_supercell, it is now easy to find the ground state. Plot the system again, now including "ghost" spins out to 12Å, to verify that the magnetic order is consistent with FeI₂.
sys_min = reshape_supercell(sys, [1 0 0; 0 2 1; 0 -2 1])
randomize_spins!(sys_min)
minimize_energy!(sys_min);
plot_spins(sys_min; color=[S[3] for S in sys_min.dipoles], ghost_radius=12)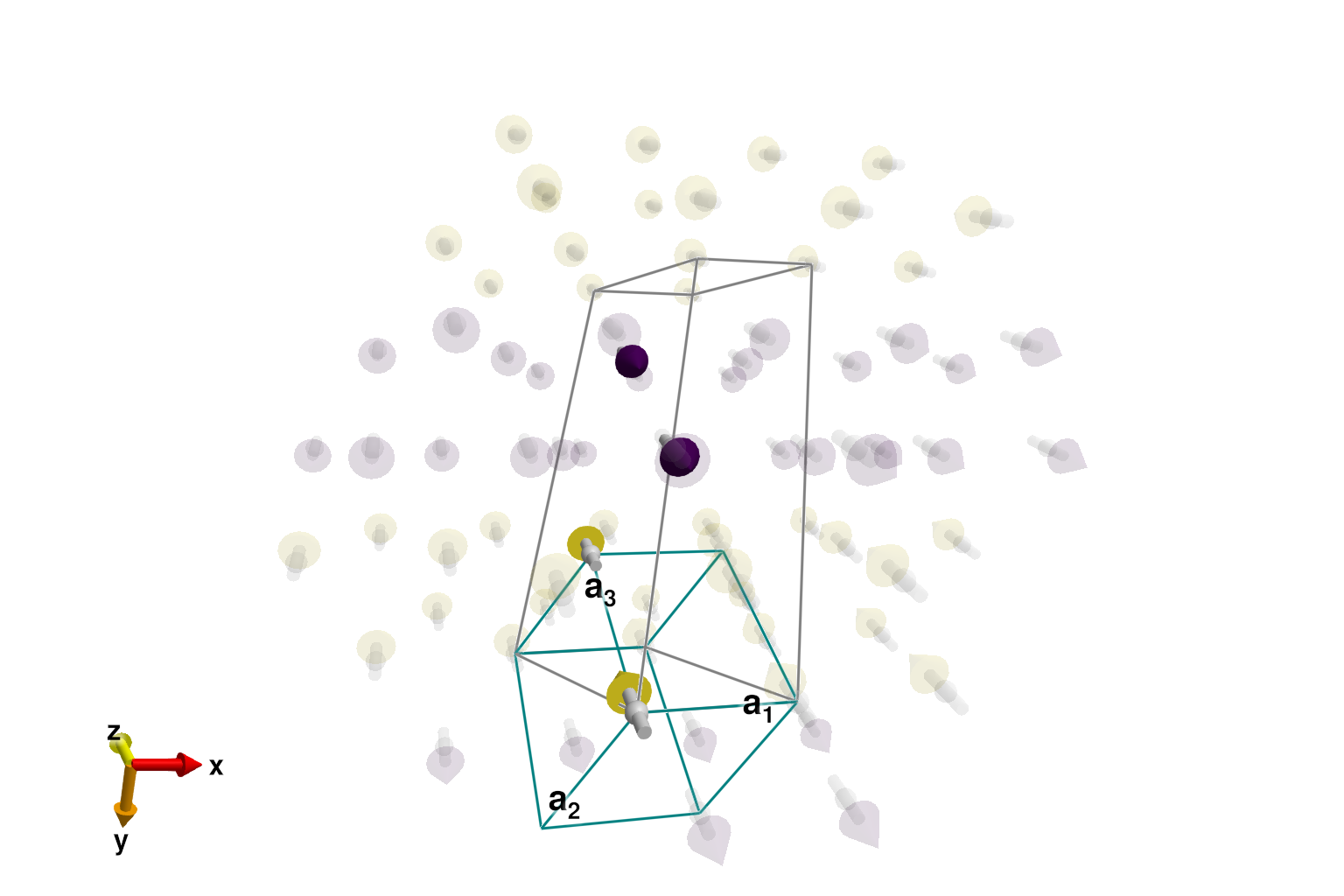
Spin wave theory
Now that the system has been relaxed to an energy minimized ground state, we can calculate the spin wave spectrum. Because we are working with a system of SU(3) coherent states, this calculation will require a multi-flavor boson generalization of the usual spin wave theory.
swt = SpinWaveTheory(sys_min; measure=ssf_perp(sys_min))SpinWaveTheory [SU(3)]
4 atoms
Calculate and plot the spectrum along a momentum-space path that connects a sequence of high-symmetry $𝐪$-points. This interface abstracts over the underlying calculator type.
qs = [[0,0,0], [1,0,0], [0,1,0], [1/2,0,0], [0,1,0], [0,0,0]]
path = q_space_path(cryst, qs, 500)
res = intensities_bands(swt, path)
plot_intensities(res; units, title="Single Crystal Bands")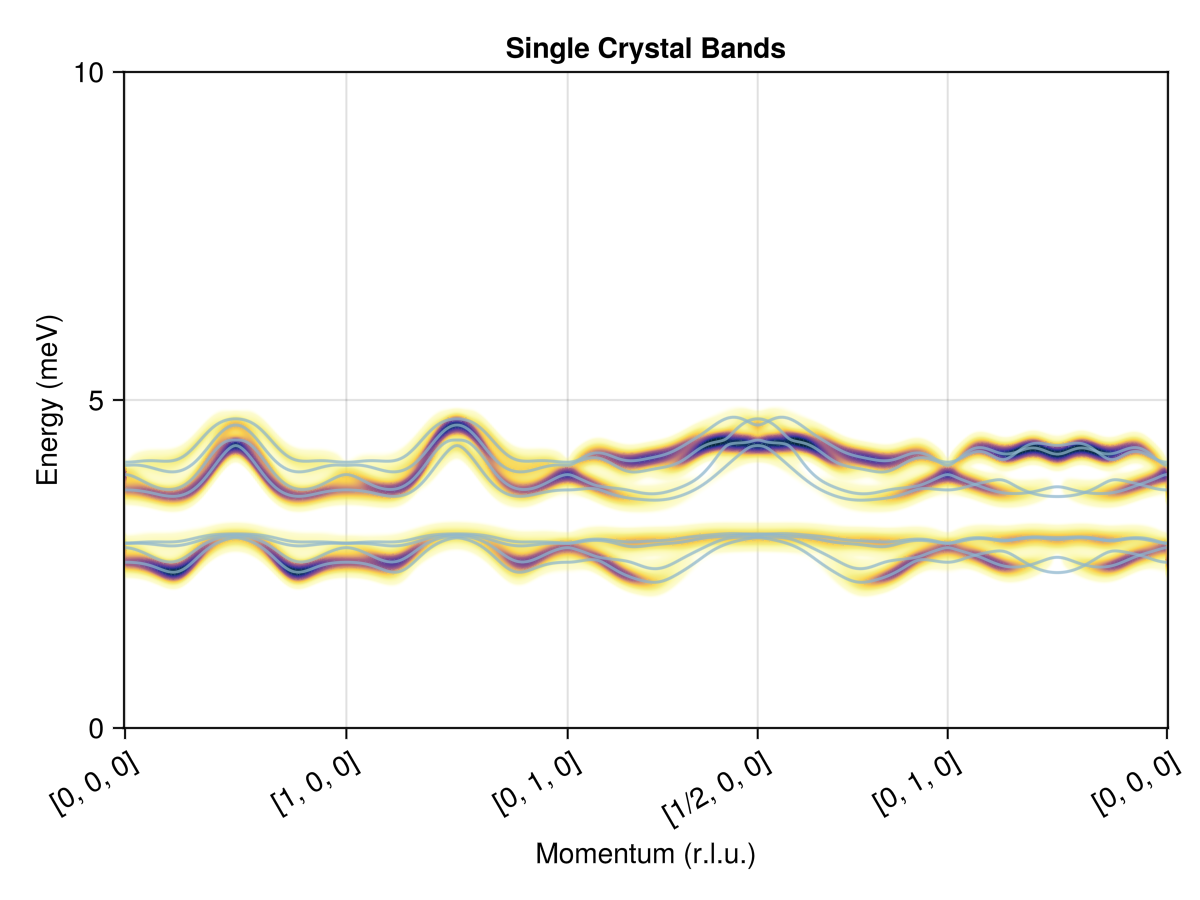
To make direct comparison with inelastic neutron scattering (INS) data, we must account for empirical broadening of the data. Model this using a lorentzian kernel, with a full-width at half-maximum of 0.3 meV.
kernel = lorentzian(fwhm=0.3)
energies = range(0, 10, 300); # 0 < ω < 10 (meV)Also, a real FeI₂ sample will exhibit competing magnetic domains. We use domain_average to average over the three possible domain orientations. This involves 120° rotations about the axis $\hat{z} = [0, 0, 1]$ in global Cartesian coordinates.
rotations = [([0,0,1], n*(2π/3)) for n in 0:2]
weights = [1, 1, 1]
res = domain_average(cryst, path; rotations, weights) do path_rotated
intensities(swt, path_rotated; energies, kernel)
end
plot_intensities(res; units, colormap=:viridis, title="Domain Averaged Intensities")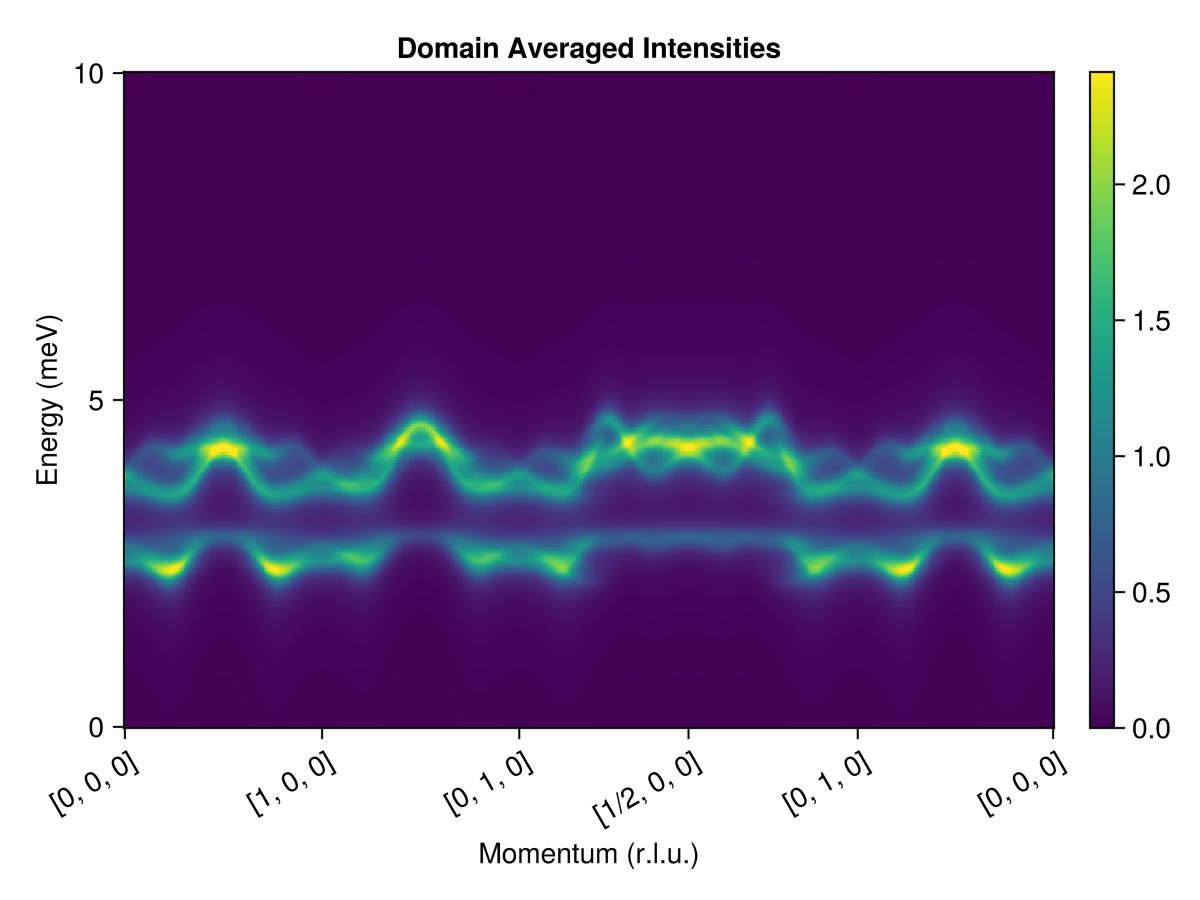
This result can be directly compared to experimental neutron scattering data from Bai et al.
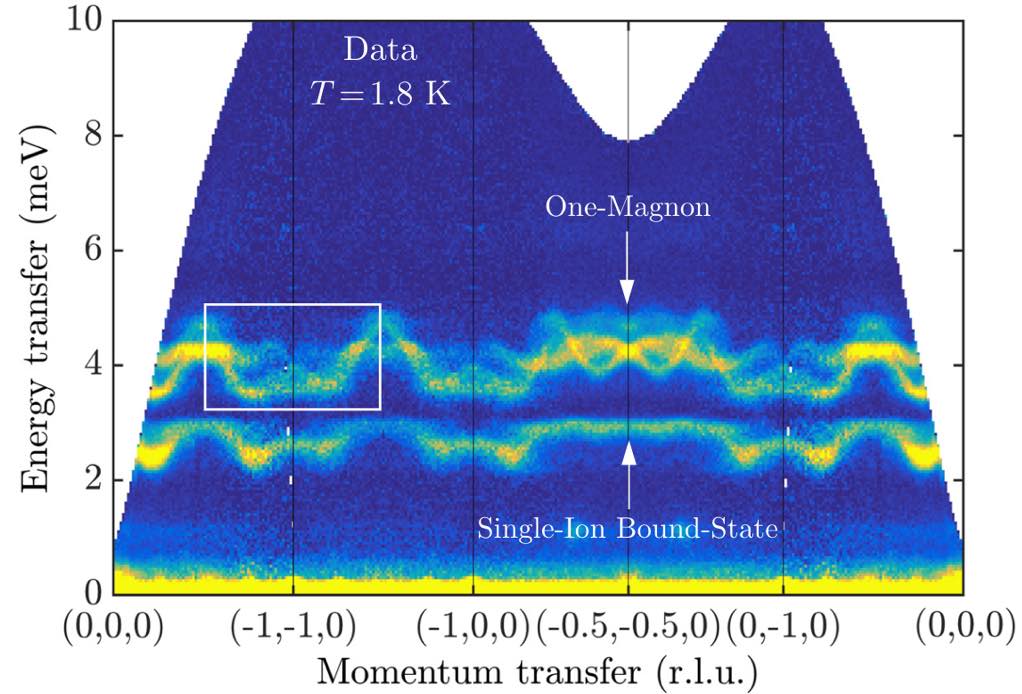
(The publication figure used a non-standard coordinate system to label the wave vectors.)
To get this agreement, the theory of SU(3) coherent states is essential. The lower band has large quadrupolar character, and arises from the strong easy-axis anisotropy of FeI₂.
An interesting exercise is to repeat the same study, but using :dipole mode instead of :SUN. That alternative choice would constrain the coherent state dynamics to the space of dipoles only, and the flat band of single-ion bound states would be missing.