Download this example as Julia file or Jupyter notebook.

SW18 - Distorted kagome

This is a Sunny port of SpinW Tutorial 18, originally authored by Goran Nilsen and Sandor Toth. This tutorial illustrates spin wave calculations for KCu₃As₂O₇(OD)₃. The Cu ions are arranged in a distorted kagome lattice and exhibit an incommensurate helical magnetic order, as described in G. J. Nilsen, et al., Phys. Rev. B 89, 140412 (2014). The model follows Toth and Lake, J. Phys.: Condens. Matter 27, 166002 (2015).

using Sunny, GLMakie

Build the distorted kagome crystal, with spacegroup 12 ("C 1 2/m 1" setting).

units = Units(:meV, :angstrom)
latvecs = lattice_vectors(10.2, 5.94, 7.81, 90, 117.7, 90)
positions = [[0, 0, 0], [1/4, 1/4, 0]]
types = ["Cu1", "Cu2"]
cryst = Crystal(latvecs, positions, "C 1 2/m 1"; types)
view_crystal(cryst)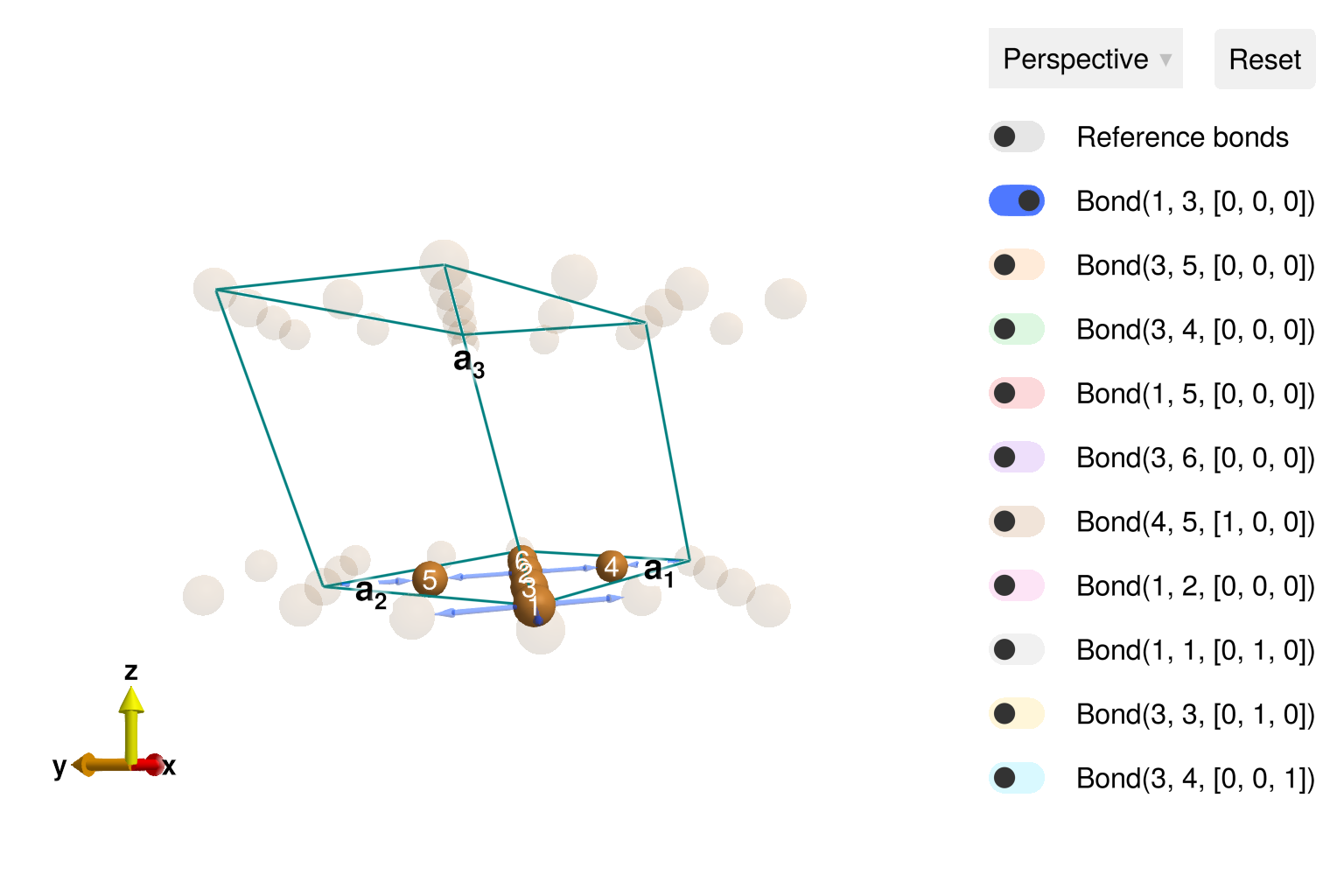

Define the interactions.

moments = [1 => Moment(s=1/2, g=2), 3 => Moment(s=1/2, g=2)]
sys = System(cryst, moments, :dipole)
J   = -2
Jp  = -1
Jab = 0.75
Ja  = -J/.66 - Jab
Jip = 0.01
set_exchange!(sys, J, Bond(1, 3, [0, 0, 0]))
set_exchange!(sys, Jp, Bond(3, 5, [0, 0, 0]))
set_exchange!(sys, Ja, Bond(3, 4, [0, 0, 0]))
set_exchange!(sys, Jab, Bond(1, 2, [0, 0, 0]))
set_exchange!(sys, Jip, Bond(3, 4, [0, 0, 1]))

Use minimize_spiral_energy! to optimize the generalized spiral order. This determines the propagation wavevector k and fits the spin values within the unit cell. One must provide a fixed axis perpendicular to the polarization plane. For this system, all interactions are rotationally invariant and the axis vector is arbitrary. In other cases, a good axis will frequently be determined from symmetry considerations.

axis = [0, 0, 1]
randomize_spins!(sys)
k = minimize_spiral_energy!(sys, axis; k_guess=randn(3))
plot_spins(sys; ndims=2)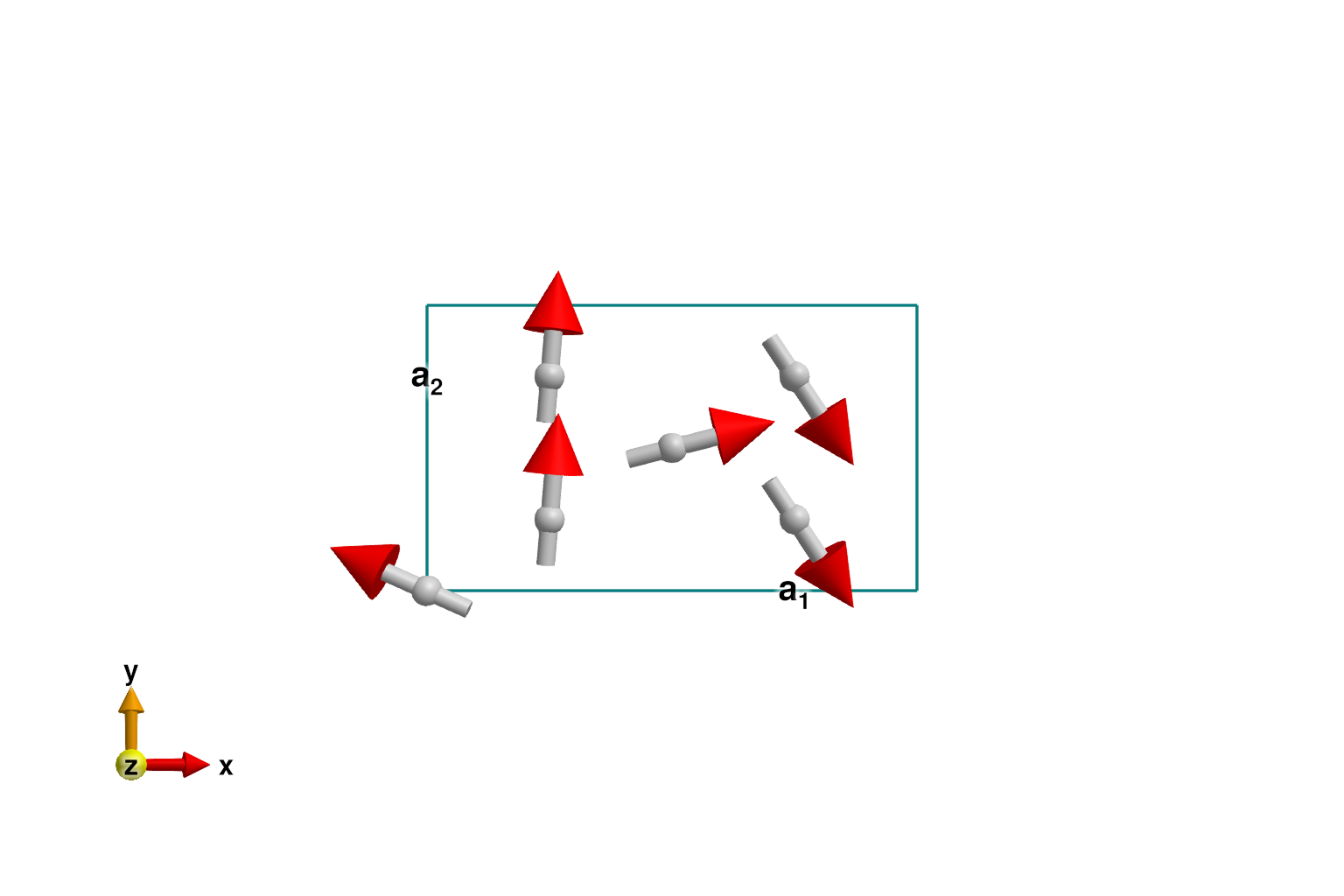

If successful, the optimization process will find one two propagation wavevectors, ±k_ref, with opposite chiralities. In this system, the spiral_energy_per_site is independent of chirality.

k_ref = [0.785902495, 0.0, 0.107048756]
k_ref_alt = [1, 0, 1] - k_ref
@assert isapprox(k, k_ref; atol=1e-6) || isapprox(k, k_ref_alt; atol=1e-6)
@assert spiral_energy_per_site(sys; k, axis) ≈ -0.78338383838

Check the energy with a real-space calculation using a large magnetic cell. First, we must determine a lattice size for which k becomes approximately commensurate.

suggest_magnetic_supercell([k_ref]; tol=1e-3)

Possible magnetic supercell in multiples of lattice vectors:

    [1 0 -7; 0 1 0; 2 0 14]

for the rationalized wavevectors:

    [[11/14, 0, 3/28]]

Resize the system as suggested and perform a real-space calculation. Working with a commensurate wavevector increases the energy slightly. The precise value might vary from run-to-run due to trapping in a local energy minimum.

new_shape = [14 0 1; 0 1 0; 0 0 2]
sys2 = reshape_supercell(sys, new_shape)
randomize_spins!(sys2)
minimize_energy!(sys2)
energy_per_site(sys2)

-0.7833837597216421

Return to the original system (with a single chemical cell) and construct SpinWaveTheorySpiral for calculations on the incommensurate spiral phase.

measure = ssf_perp(sys; apply_g=false)
swt = SpinWaveTheorySpiral(sys; measure, k, axis)

SpinWaveTheorySpiral(SpinWaveTheory(System([Dipole mode], Supercell (1×1×1)×6, Energy per site -0.3888), Sunny.SWTDataDipole(StaticArraysCore.SMatrix{3, 3, Float64, 9}[[0.20343529137242577 0.3544651931949604 -0.9126710848040906; 0.45429860984161563 0.7915688739038765 0.40869486290204865; 0.867310126379366 -0.49776816358602954 -1.732108730680212e-12], [0.012835414965051029 -0.2486068634064537 0.968519426542328; -0.04993753261269094 0.9672311628697852 0.2489379850688122; -0.9986698628471931 -0.05156069278790412 -6.5360437582332645e-12], [0.9235791227236043 -0.3739535796686617 0.08461869960057186; -0.07843337300742292 0.031757366401675736 0.9964134060107322; -0.37529962705520553 -0.9269035494226051 -3.4144337003474077e-13], [0.817470018166897 0.15542534332807081 0.554604121919018; 0.5448436856346364 0.10359097583105673 -0.8321143358640297; -0.1867836385293939 0.9824010751102225 -5.354322370822248e-12], [0.8308759227537308 -0.5499862513431595 0.0846186995978804; -0.07056071274008513 0.04670663913457611 0.9964134060109608; -0.551965929026193 -0.8338666639183101 -2.3544997582850745e-12], [0.832053292138642 -0.010079037107484168 0.5546041219214242; 0.5545634362855545 -0.006717677231882594 -0.8321143358624259; 0.012112562751366652 0.9999266402209686 -3.536665234905941e-12]], StaticArraysCore.SVector{3, Float64}[[0.20343529137242577, 0.3544651931949604, -0.9126710848040906] [0.012835414965051029, -0.2486068634064537, 0.968519426542328] … [0.8308759227537308, -0.5499862513431595, 0.0846186995978804] [0.832053292138642, -0.010079037107484168, 0.5546041219214242]; [0.45429860984161563, 0.7915688739038765, 0.40869486290204865] [-0.04993753261269094, 0.9672311628697852, 0.2489379850688122] … [-0.07056071274008513, 0.04670663913457611, 0.9964134060109608] [0.5545634362855545, -0.006717677231882594, -0.8321143358624259]; [0.867310126379366, -0.49776816358602954, -1.732108730680212e-12] [-0.9986698628471931, -0.05156069278790412, -6.5360437582332645e-12] … [-0.551965929026193, -0.8338666639183101, -2.3544997582850745e-12] [0.012112562751366652, 0.9999266402209686, -3.536665234905941e-12]], Sunny.StevensExpansion[Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0)], [0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 0.7071067811865476]), MeasureSpec, 1.0e-8), [0.21409750546128162, 5.337605618165189e-13, 0.8929512472446745], 3, [0.0, 0.0, 1.0], Matrix{StaticArraysCore.SMatrix{3, 3, ComplexF64, 9}}[[[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; … ; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] … [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]]])

Plot intensities for a path through $𝐪$-space.

qs = [[0,0,0], [1,0,0]]
path = q_space_path(cryst, qs, 400)
res = intensities_bands(swt, path)
plot_intensities(res; units)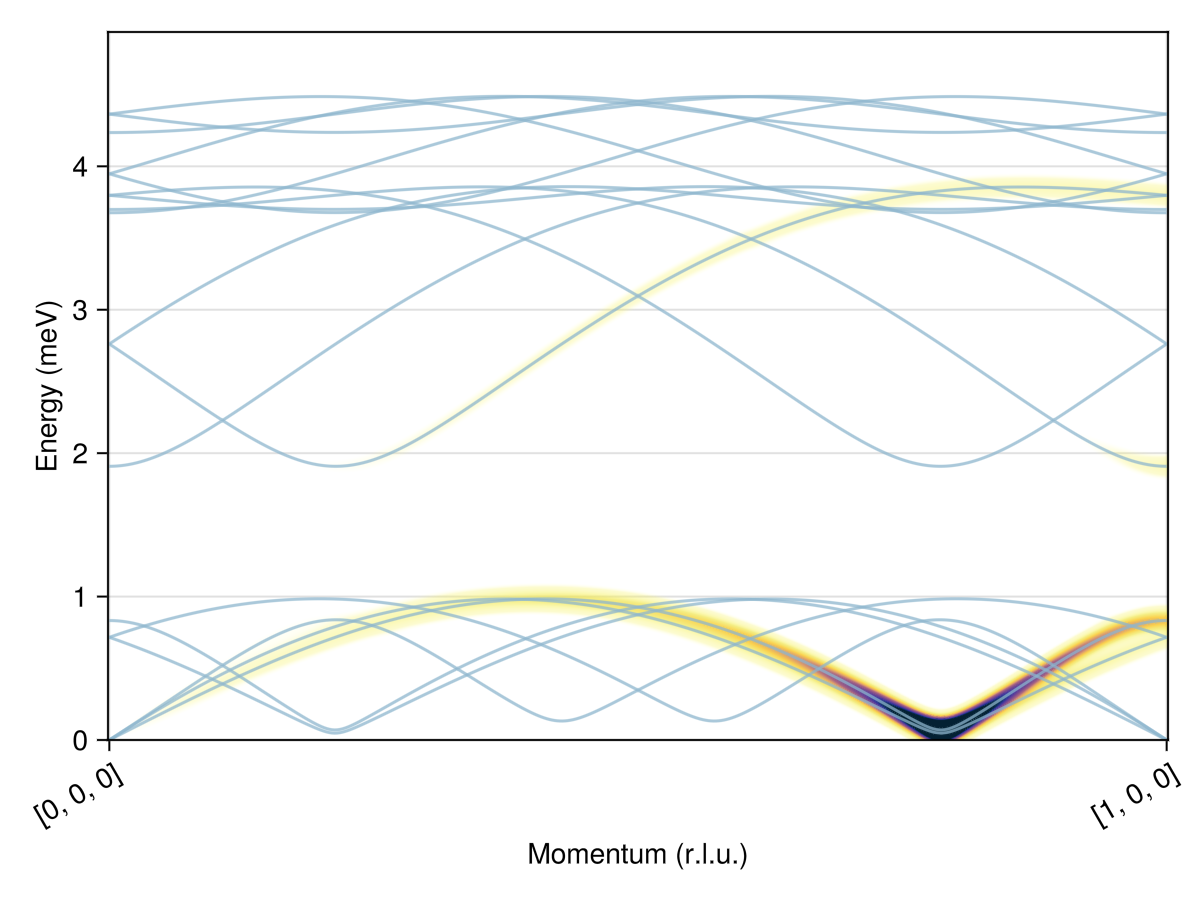

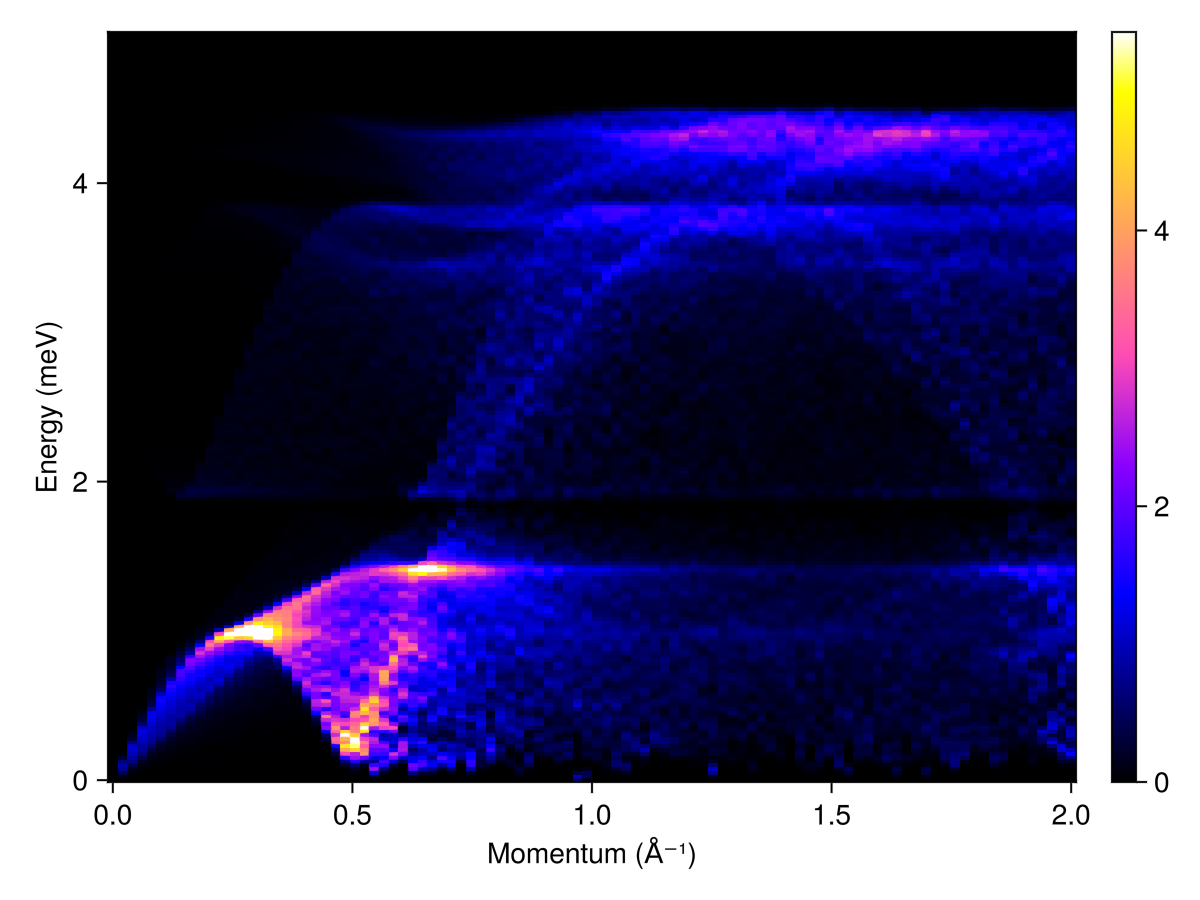
Plot the powder-averaged intensities

radii = range(0, 2, 100) # (1/Å)
energies = range(0, 5, 200)
kernel = gaussian(fwhm=0.05)
res = powder_average(cryst, radii, 400) do qs
    intensities(swt, qs; energies, kernel)
end
plot_intensities(res; units)