GitHub

Download this example as Julia file or Jupyter notebook.

SW08 - √3×√3 kagome antiferromagnet

This is a Sunny port of SpinW Tutorial 8, originally authored by Bjorn Fak and Sandor Toth. It calculates the linear spin wave theory spectrum for the $\sqrt{3} \times \sqrt{3}$ order of a kagome antiferromagnet.

Load Sunny and the GLMakie plotting package

using Sunny, GLMakie

Define the chemical cell of a kagome lattice with spacegroup 147 (P-3).

units = Units(:meV, :angstrom)
latvecs = lattice_vectors(6, 6, 40, 90, 90, 120)
cryst = Crystal(latvecs, [[1/2, 0, 0]], 147)
view_crystal(cryst; ndims=2)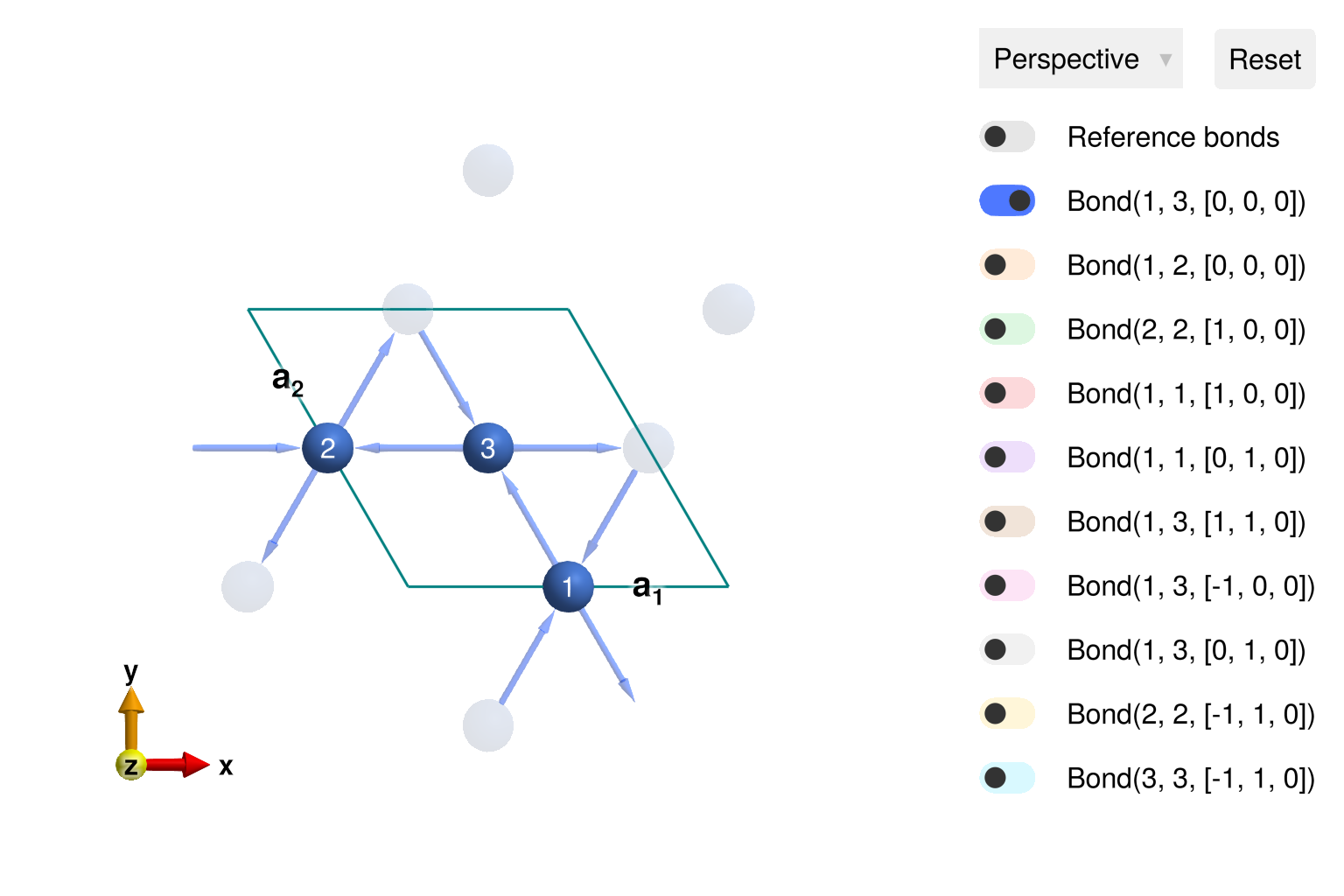
Example block output

Construct a spin system with nearest neighbor antiferromagnetic exchange.

sys = System(cryst, [1 => Moment(s=1, g=2)], :dipole)
J = 1.0
set_exchange!(sys, J, Bond(2, 3, [0, 0, 0]))

Initialize to an energy minimizing magnetic structure, for which nearest-neighbor spins are at 120° angles.

set_dipole!(sys, [cos(0), sin(0), 0], (1, 1, 1, 1))
set_dipole!(sys, [cos(0), sin(0), 0], (1, 1, 1, 2))
set_dipole!(sys, [cos(2π/3), sin(2π/3), 0], (1, 1, 1, 3))
k = [-1/3, -1/3, 0]
axis = [0, 0, 1]
sys_enlarged = repeat_periodically_as_spiral(sys, (3, 3, 1); k, axis)
plot_spins(sys_enlarged; ndims=2)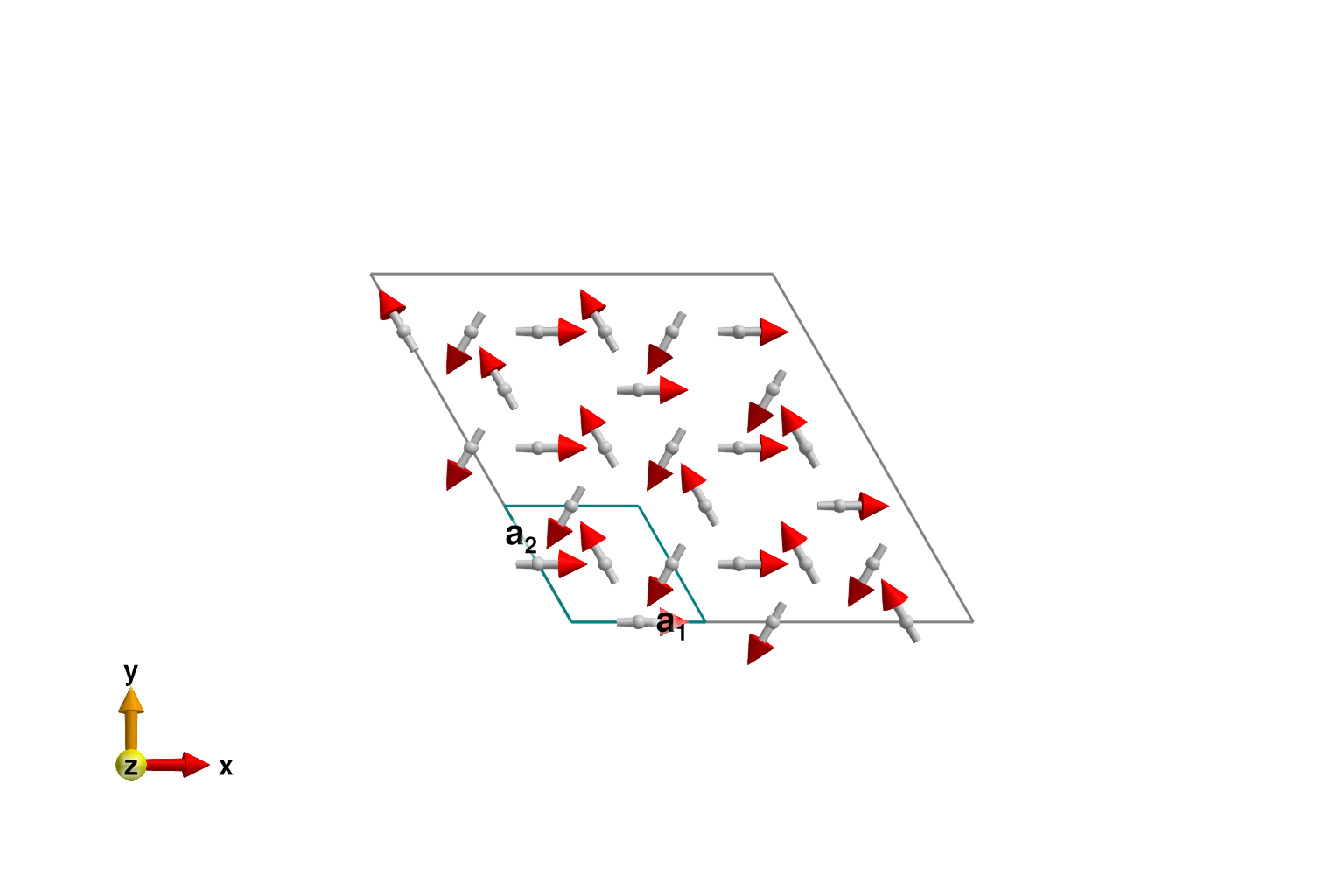
Example block output

Check energy per site. Each site participates in 4 bonds with energy $J\cos(2π/3)$. Factor of 1/2 avoids double counting. The two calculation methods agree.

@assert energy_per_site(sys_enlarged) ≈ (4/2)*J*cos(2π/3)
@assert spiral_energy_per_site(sys; k, axis) ≈ (4/2)*J*cos(2π/3)

Calculate and plot intensities for a path through $𝐪$-space using two calculation methods. The two methods agree in intensity, but the "supercell method" gives rise to ghost modes in the dispersion that have zero intensity.

qs = [[-1/2,0,0], [0,0,0], [1/2,1/2,0]]
path = q_space_path(cryst, qs, 400)

fig = Figure(size=(768, 300))
swt = SpinWaveTheory(sys_enlarged; measure=ssf_perp(sys_enlarged))
res = intensities_bands(swt, path)
plot_intensities!(fig[1, 1], res; units, saturation=0.5,title="Supercell method")
swt = SpinWaveTheorySpiral(sys; measure=ssf_perp(sys), k, axis)
res = intensities_bands(swt, path)
plot_intensities!(fig[1, 2], res; units, saturation=0.5, title="Spiral method")
fig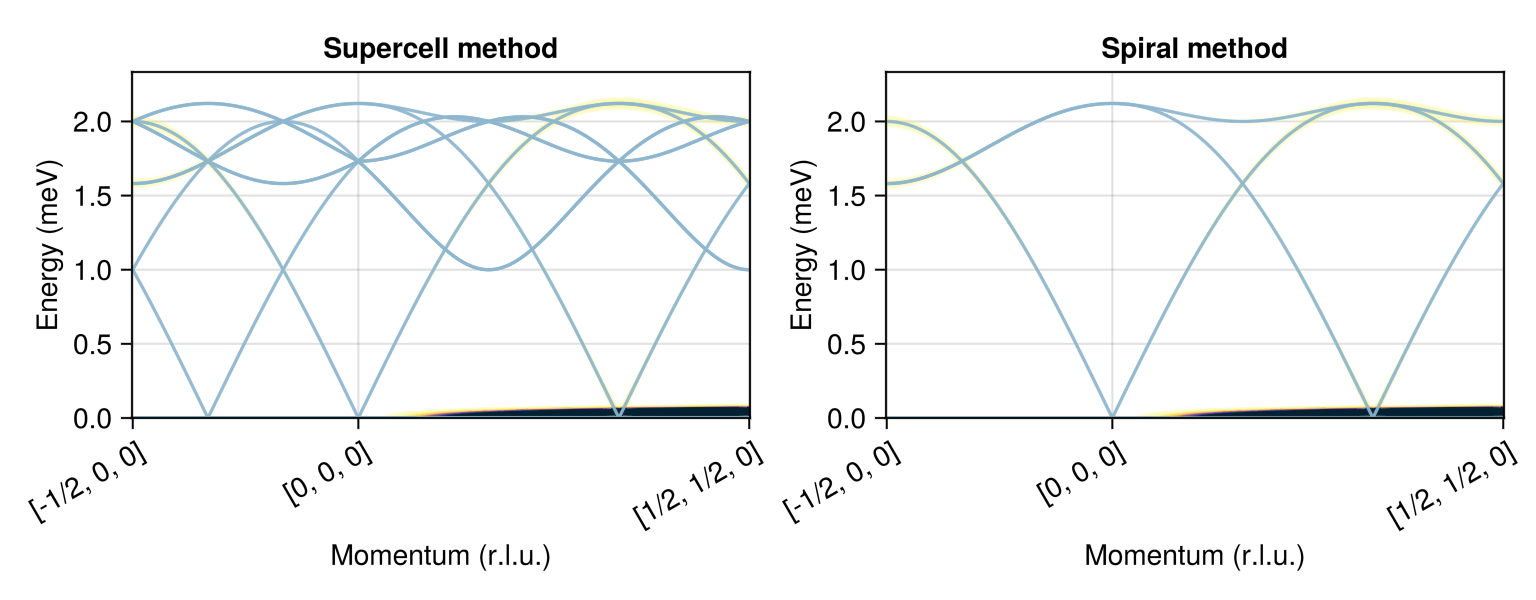
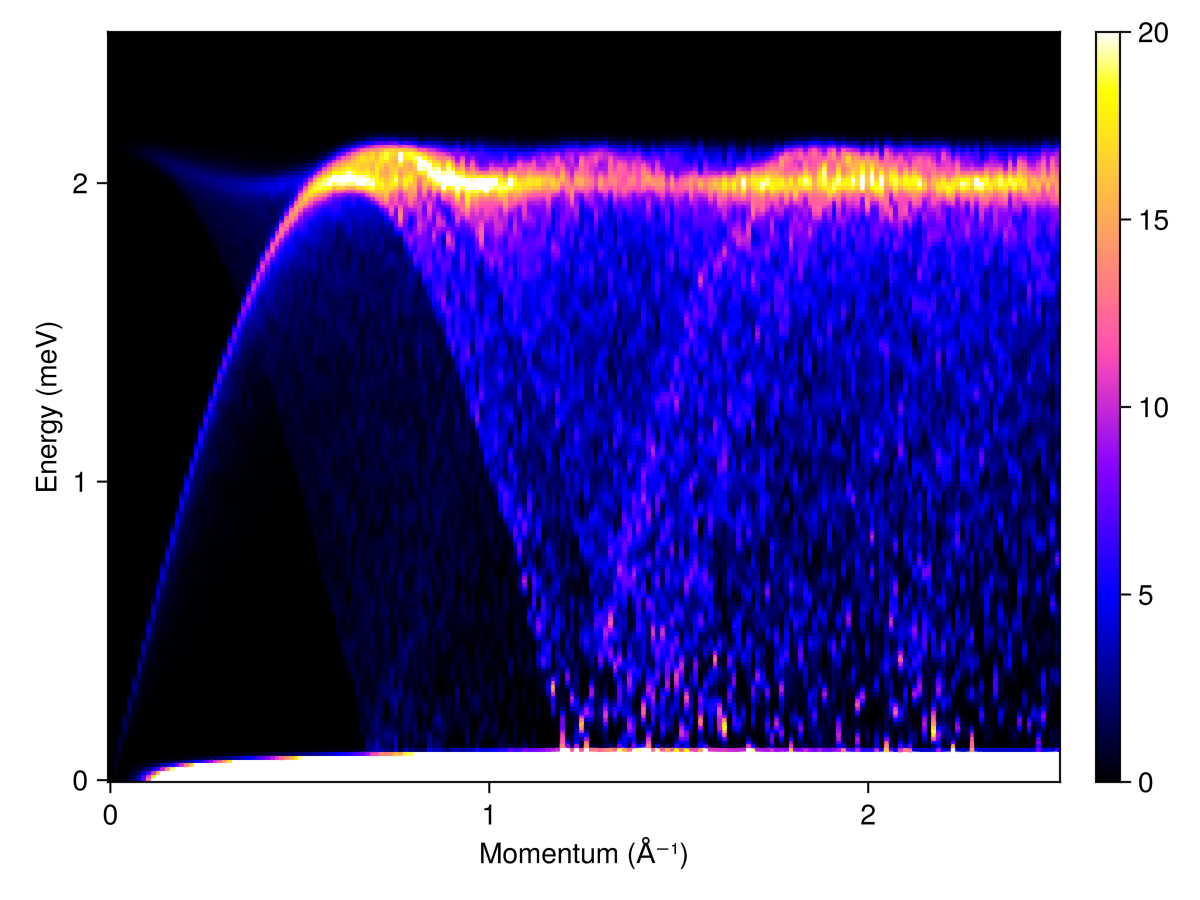
Example block output

Calculate and plot the powder averaged spectrum. Continuing to use the "spiral method", this calculation executes in about two seconds. Because the intensities are dominated by a flat band at zero energy transfer, select an empirical colorrange that brings the lower-intensity features into focus.

radii = range(0, 2.5, 200)
energies = range(0, 3, 200)
kernel = gaussian(fwhm=0.05)
res = powder_average(cryst, radii, 200) do qs
    intensities(swt, qs; energies, kernel)
end
plot_intensities(res; units, colorrange=(0,20))
Example block output