Download this example as Julia file or Jupyter notebook.

SW11 - La₂CuO₄

This is a Sunny port of SpinW Tutorial 11, originally authored by Sandor Toth. It calculates the spin wave spectrum of La₂CuO₄.

Load packages

using Sunny, GLMakie

Build a square lattice for the the Cu²⁺ atoms. The lattice constant 1 Å is selected arbitrarily.

units = Units(:meV, :angstrom)
latvecs = lattice_vectors(1, 1, 10, 90, 90, 90)
positions = [[0, 0, 0]]
types = ["Cu"]
cryst = Crystal(latvecs, positions, 139; types)
view_crystal(cryst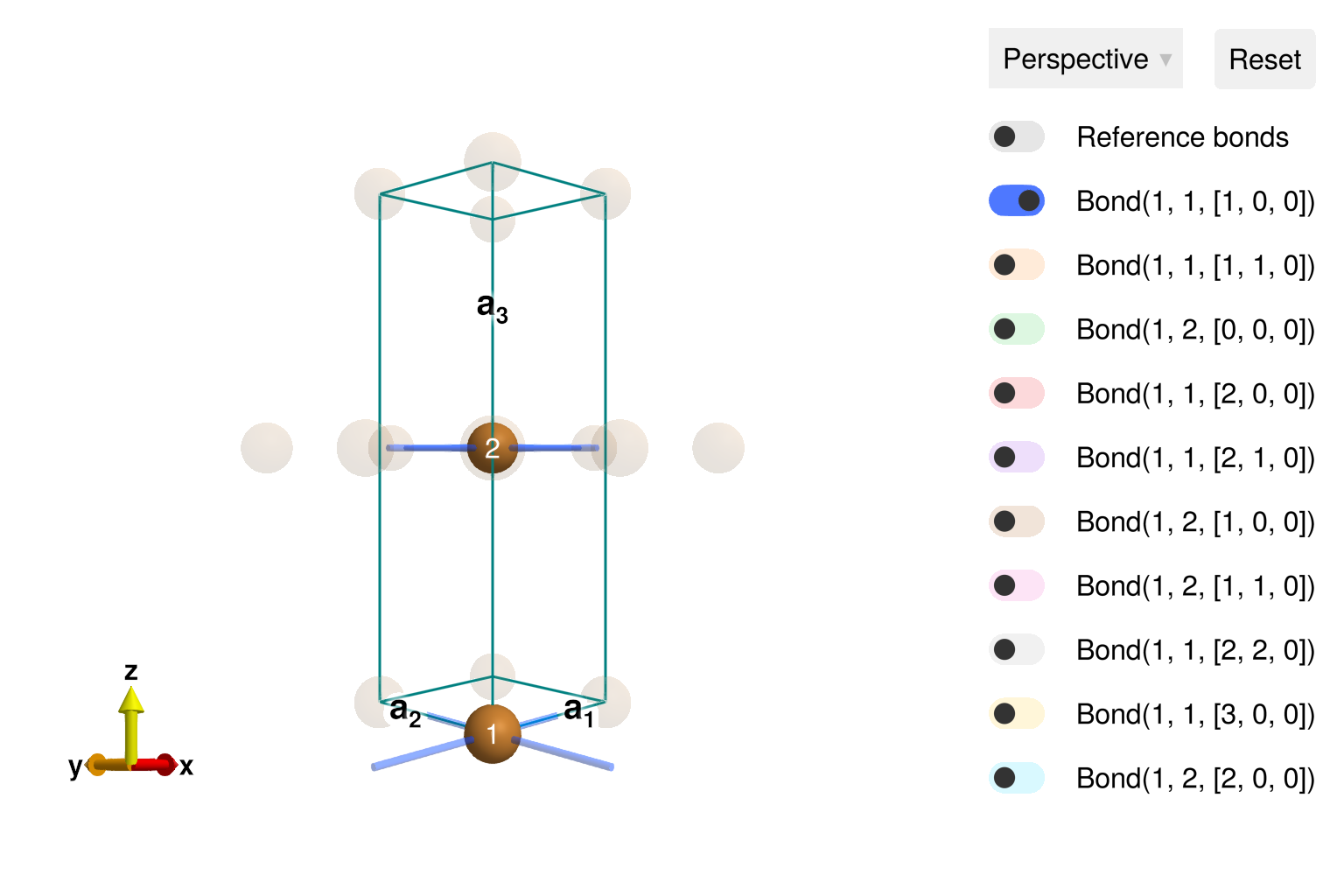; ndims=2)

Build a spin system using the exchange parameters from R. Coldea, Phys. Rev. Lett. 86, 5377 (2001).

sys = System(cryst, [1 => Moment(s=1/2, g=2)], :dipole; dims=(2, 2, 1))
J   = 138.3
Jp  = 2
Jpp = 2
Jc  = 38
set_exchange!(sys, J-Jc/2, Bond(1, 1, [1, 0, 0]))
set_exchange!(sys, Jp-Jc/4, Bond(1, 1, [1, 1, 0]))
set_exchange!(sys, Jpp, Bond(1, 1, [2, 0, 0]))

Energy minimization yields the expected Néel order

randomize_spins!(sys)
minimize_energy!(sys)
plot_spins(sys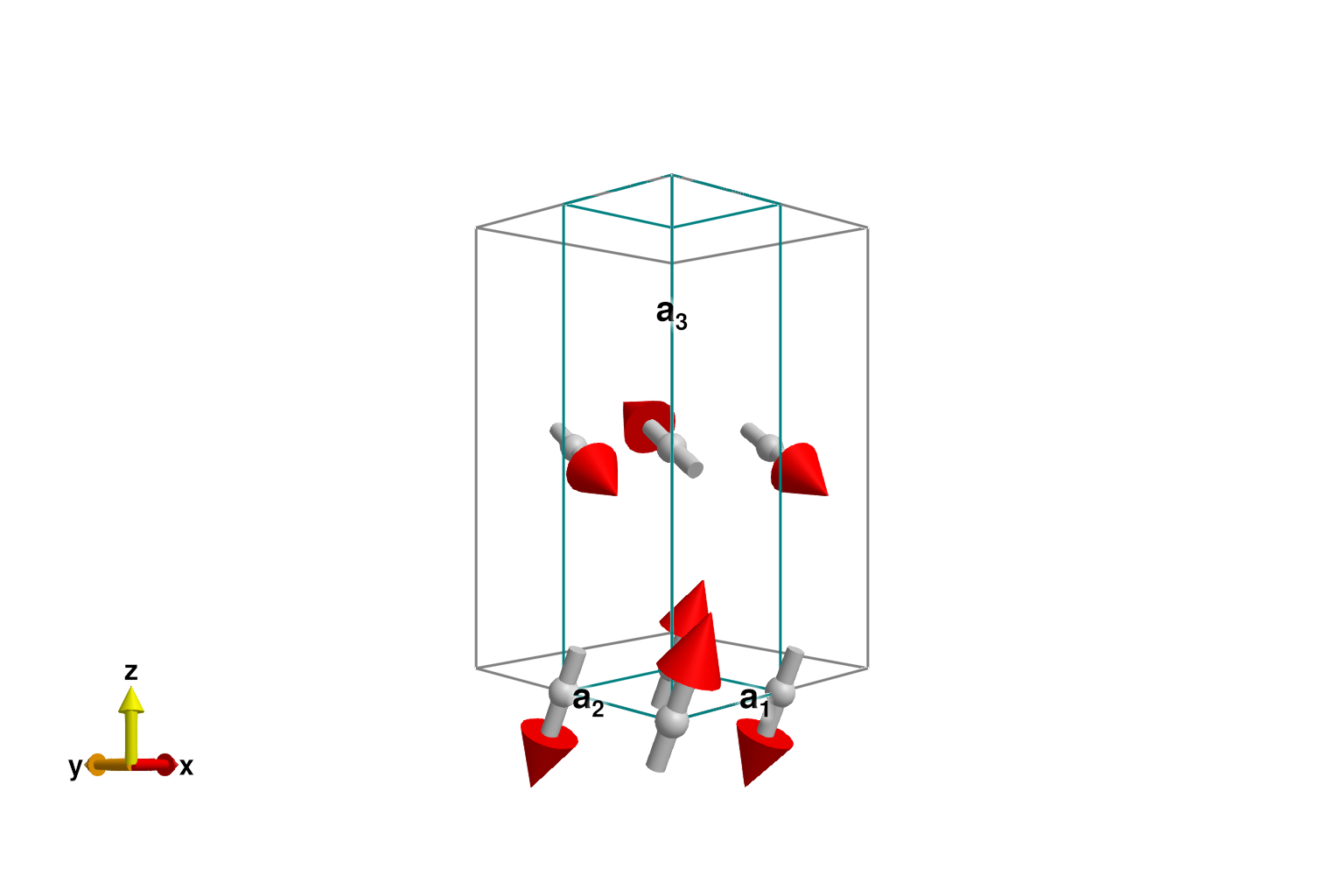; ndims=2)

Plot the spin wave spectrum for a path through $𝐪$-space. Apply a manual "quantum correction" that adjusts energy scale by the factor 1.18.

qs = [[3/4,1/4,0], [1/2, 1/2, 0], [1/2, 0, 0], [3/4, 1/4, 0], [1,0,0], [1/2 0 0]]
labels = ["P", "M", "X", "P", "Γ", "X"]
path = q_space_path(cryst, qs, 400; labels)
energies = range(0, 320, 400)
swt = SpinWaveTheory(sys; measure=ssf_perp(sys))
res = intensities(swt, path; energies, kernel=gaussian(fwhm=35))
res.energies .*= 1.18
plot_intensities(res; units)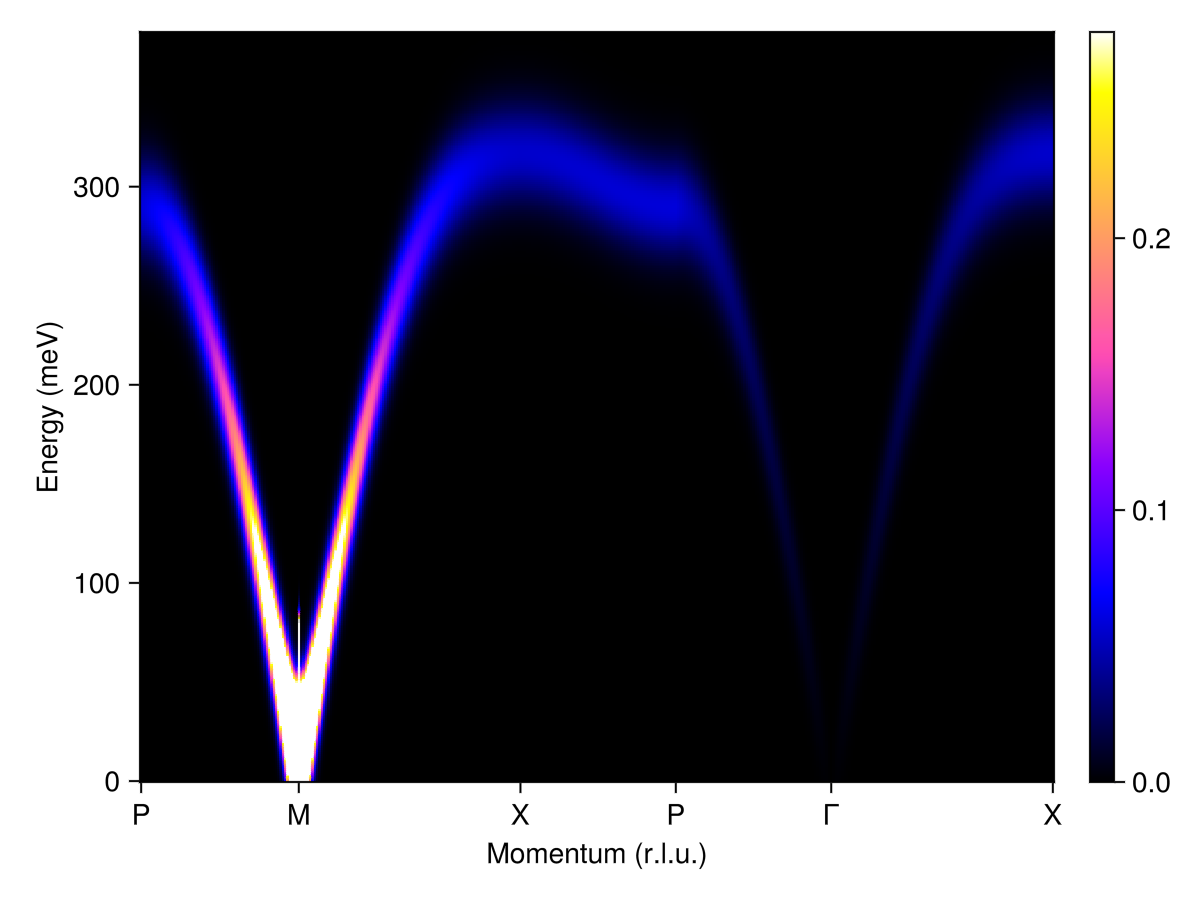

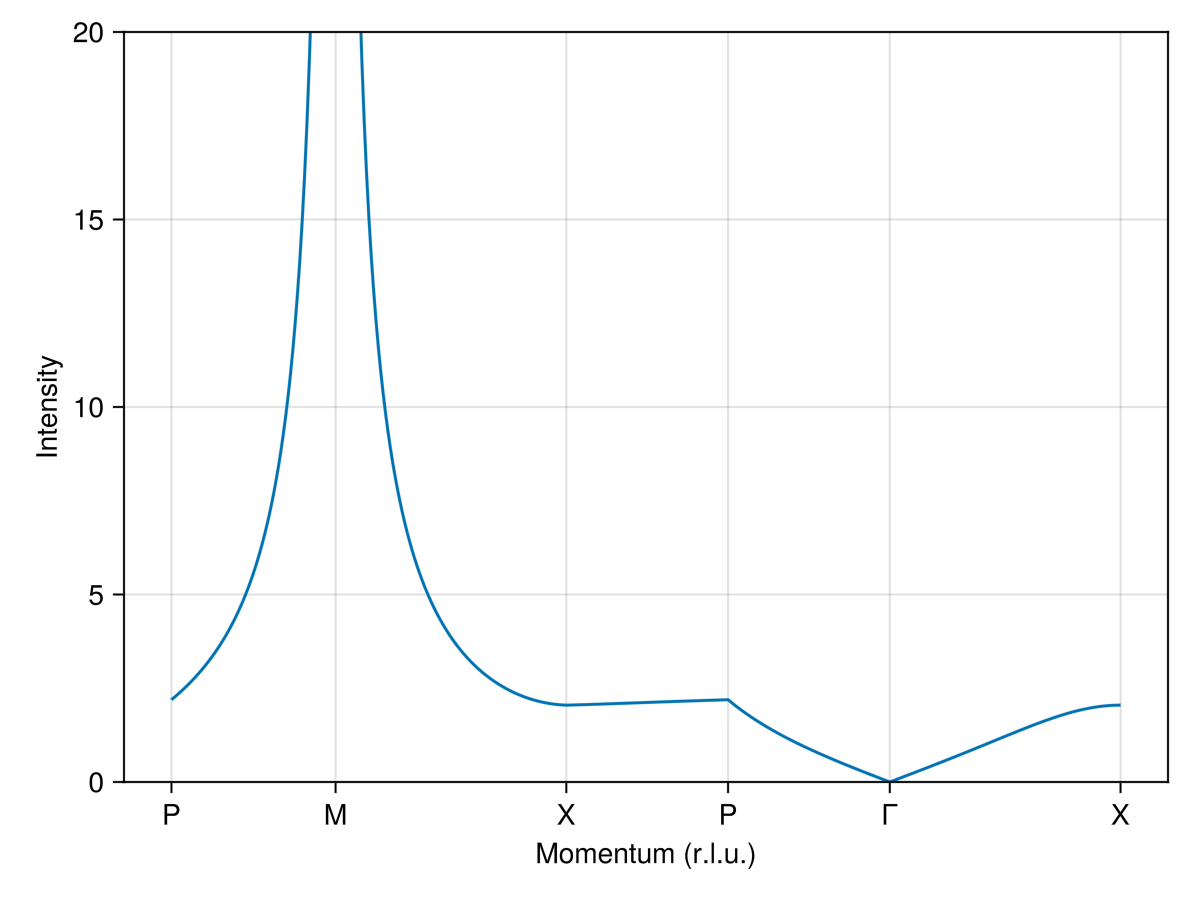
Plot instantaneous itensities, integrated over ω.

res = intensities_static(swt, path)
plot_intensities(res; colorrange=(0,20), units)