Download this example as Julia file or Jupyter notebook.

SW15 - Ba₃NbFe₃Si₂O₁₄

This is a Sunny port of SpinW Tutorial 15, originally authored by Sandor Toth. It calculates the linear spin wave theory spectrum of Ba₃NbFe₃Si₂O₁₄. The ground state is an incommensurate spiral, which can be directly studied using the functions minimize_spiral_energy! and SpinWaveTheorySpiral.

Load packages

using Sunny, GLMakie

Specify the Ba₃NbFe₃Si₂O₁₄ Crystal cell following Marty et al., Phys. Rev. Lett. 101, 247201 (2008).

units = Units(:meV, :angstrom)
a = b = 8.539 # (Å)
c = 5.2414
latvecs = lattice_vectors(a, b, c, 90, 90, 120)
types = ["Fe", "Nb", "Ba", "Si", "O", "O", "O"]
positions = [[0.24964,0,0.5], [0,0,0], [0.56598,0,0], [2/3,1/3,0.5220],
             [2/3,1/3,0.2162], [0.5259,0.7024,0.3536], [0.7840,0.9002,0.7760]]
langasite = Crystal(latvecs, positions, 150; types)
cryst = subcrystal(langasite, "Fe")
view_crystal(cryst)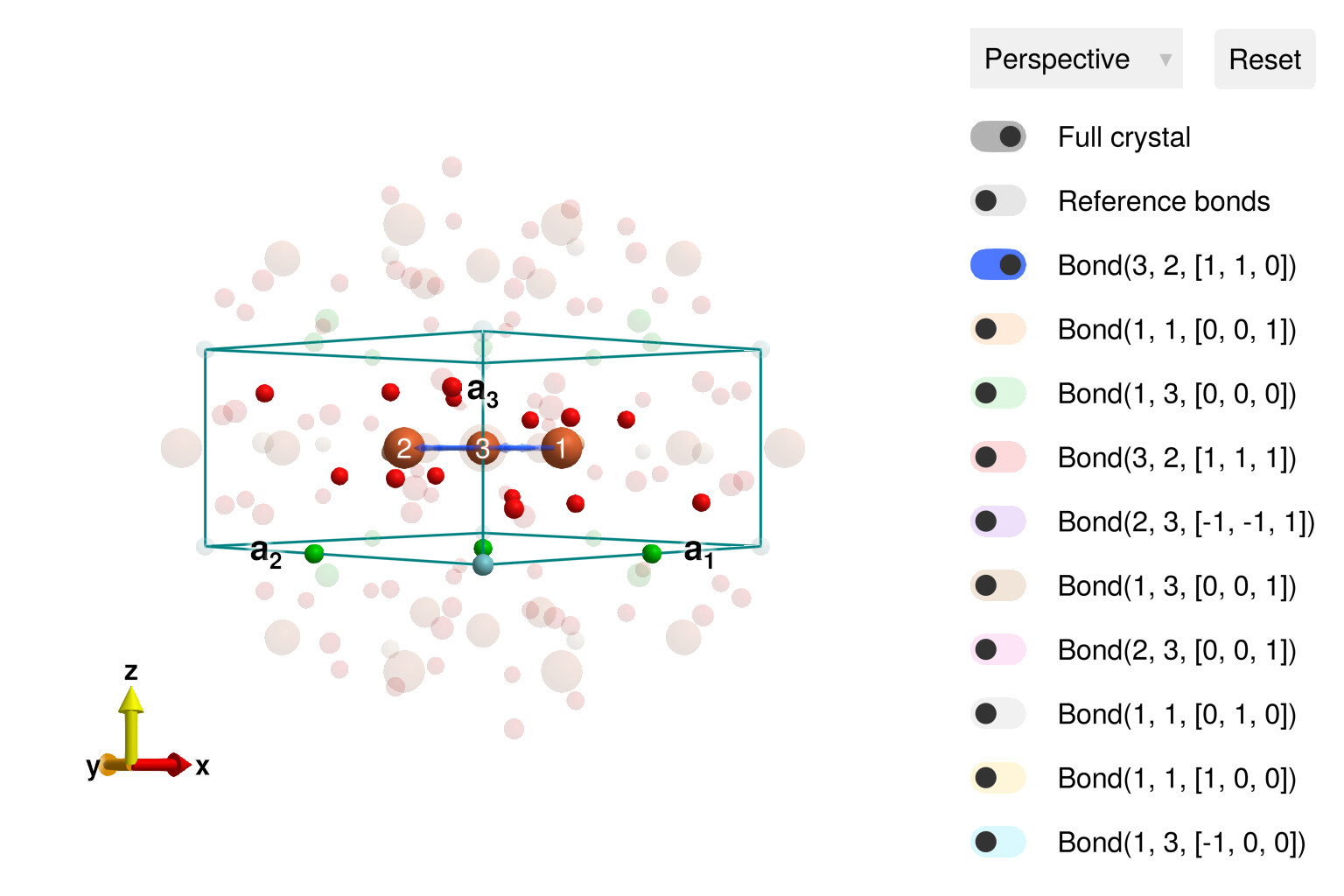

Create a System and set exchange interactions as parametrized in Loire et al., Phys. Rev. Lett. 106, 207201 (2011).

sys = System(cryst, [1 => Moment(s=5/2, g=2)], :dipole)
J₁ = 0.85
J₂ = 0.24
J₃ = 0.053
J₄ = 0.017
J₅ = 0.24
set_exchange!(sys, J₁, Bond(3, 2, [1,1,0]))
set_exchange!(sys, J₄, Bond(1, 1, [0,0,1]))
set_exchange!(sys, J₂, Bond(1, 3, [0,0,0]))

The final two exchanges are set according to the desired chirality $ϵ_T$ of the magnetic structure.

ϵT = -1
if ϵT == -1
    set_exchange!(sys, J₃, Bond(2, 3, [-1,-1,1]))
    set_exchange!(sys, J₅, Bond(3, 2, [1,1,1]))
elseif ϵT == 1
    set_exchange!(sys, J₅, Bond(2, 3, [-1,-1,1]))
    set_exchange!(sys, J₃, Bond(3, 2, [1,1,1]))
else
    error("Chirality must be ±1")
end

This compound is known to have a spiral order with approximate propagation wavevector $𝐤 ≈ [0, 0, 1/7]$. Search for this magnetic order with minimize_spiral_energy!. Due to reflection symmetry, one of two possible propagation wavevectors may appear, $𝐤 = ± [0, 0, 0.1426…]$. Note that $k_z = 0.1426…$ is very close to $1/7 = 0.1428…$.

axis = [0, 0, 1]
randomize_spins!(sys)
k = minimize_spiral_energy!(sys, axis)

3-element StaticArraysCore.SVector{3, Float64} with indices SOneTo(3):
  3.065613328087738e-13
 -2.5576662916386797e-13
  0.14264604656290922

We can visualize the full magnetic cell using repeat_periodically_as_spiral, which includes 7 rotated copies of the chemical cell.

sys_enlarged = repeat_periodically_as_spiral(sys, (1, 1, 7); k, axis)
plot_spins(sys_enlarged; color=[S[1] for S in sys_enlarged.dipoles])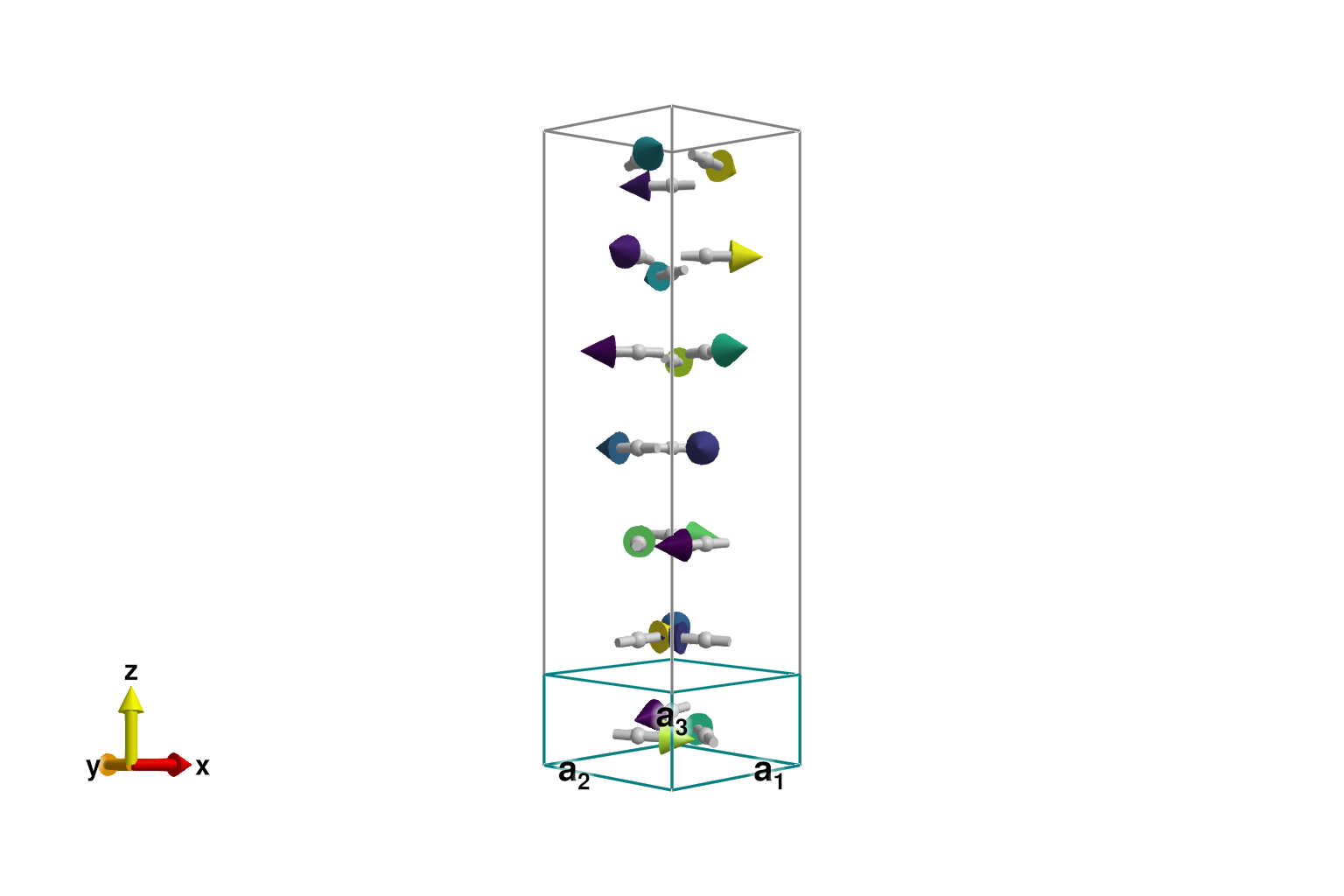

One could perform a spin wave calculation using either SpinWaveTheory on sys_enlarged, or SpinWaveTheorySpiral on the original sys. The latter has some restrictions on the interactions, but allows for our slightly incommensurate wavevector $𝐤$.

measure = ssf_perp(sys)
swt = SpinWaveTheorySpiral(sys; measure, k, axis)

SpinWaveTheorySpiral(SpinWaveTheory(System([Dipole mode], Supercell (1×1×1)×3, Energy per site 9.601), Sunny.SWTDataDipole(StaticArraysCore.SMatrix{3, 3, Float64, 9}[[0.9184188029372586 -0.3197854070888741 0.23290383385486893; -0.21995199044203498 0.07658536234087655 0.9724997707843965; -0.3288282596004794 -0.9443897371785231 1.0975126717292283e-13], [0.563034591172907 0.3953074374007352 0.7257575897490989; 0.5939767681991082 0.4170319866846718 -0.687950522146454; -0.5746160874727582 0.8184230886390605 1.6669393813271907e-11], [-0.003261942231613195 -0.28453055131660465 -0.958661423600818; 0.010989655340752474 0.958598431344345 -0.2845492486365995; 0.9999342914453776 -0.011463541844949642 -1.3476491974374968e-11]], StaticArraysCore.SVector{3, Float64}[[1.8368376058745168, -0.6395708141777481, 0.46580766770973797] [1.1260691823458138, 0.7906148748014703, 1.4515151794981977] [-0.006523884463226383, -0.5690611026332087, -1.9173228472016344]; [-0.4399039808840695, 0.15317072468175297, 1.9449995415687922] [1.1879535363982157, 0.834063973369343, -1.3759010442929074] [0.021979310681504934, 1.9171968626886888, -0.5690984972731988]; [-0.6576565192009587, -1.8887794743570459, 2.1950253434584562e-13] [-1.149232174945516, 1.6368461772781207, 3.333878762654381e-11] [1.9998685828907543, -0.022927083689899274, -2.6952983948749923e-11]], Sunny.StevensExpansion[Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0), Sunny.StevensExpansion([0.0], [0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0)], [1.5811388300841898, 1.5811388300841898, 1.5811388300841898]), MeasureSpec, 1.0e-8), [3.065613328087738e-13, -2.5576662916386797e-13, 0.14264604656290922], 3, [0.0, 0.0, 1.0], Matrix{StaticArraysCore.SMatrix{3, 3, ComplexF64, 9}}[[[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]], [[0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]; [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im] [0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im; 0.0 + 0.0im 0.0 + 0.0im 0.0 + 0.0im]]])

Calculate broadened intensities for a path $[0, 1, L]$ through reciprocal space

qs = [[0, 1, -1], [0, 1, -1+1], [0, 1, -1+2], [0, 1, -1+3]]
path = q_space_path(cryst, qs, 400)
energies = range(0, 6, 400)
res = intensities(swt, path; energies, kernel=gaussian(fwhm=0.25))
plot_intensities(res; units, saturation=0.7, colormap=:jet, title="Scattering intensities")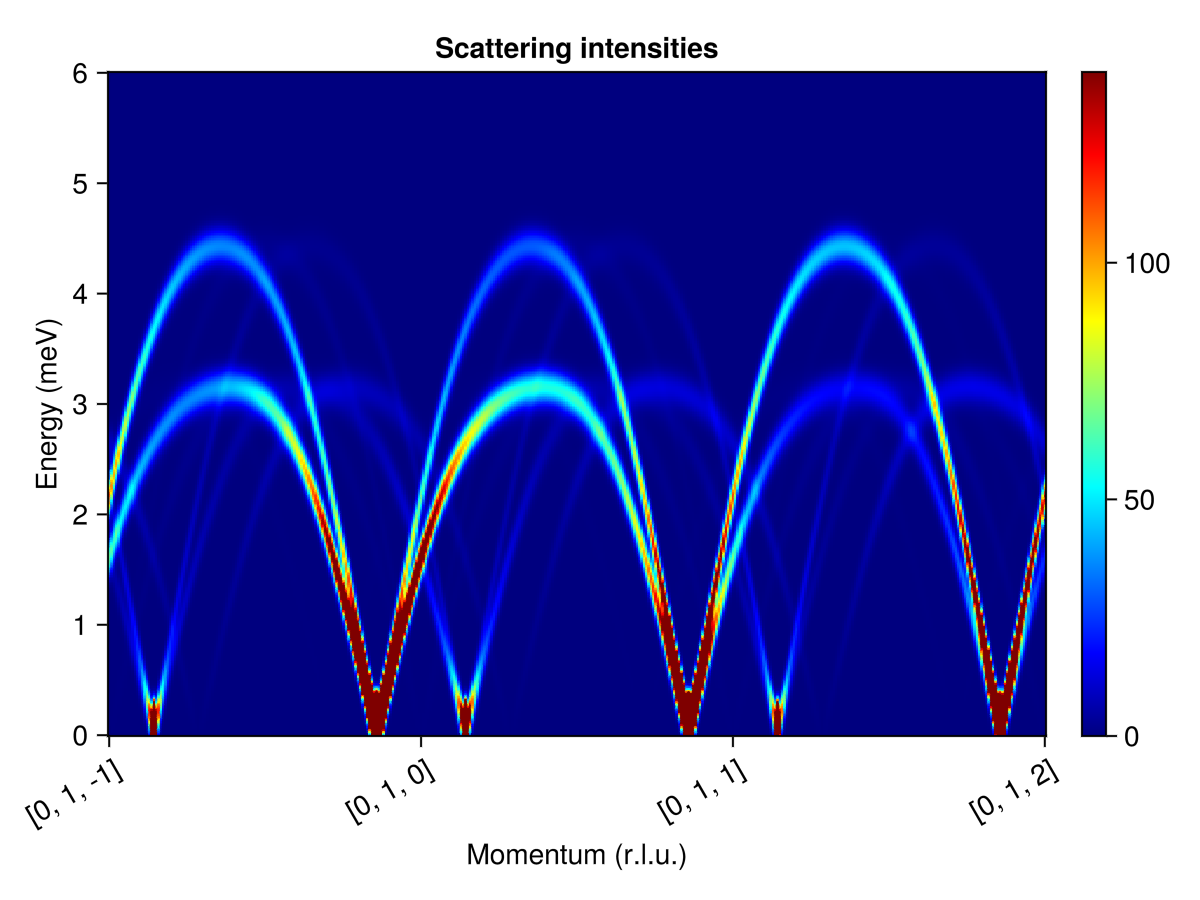

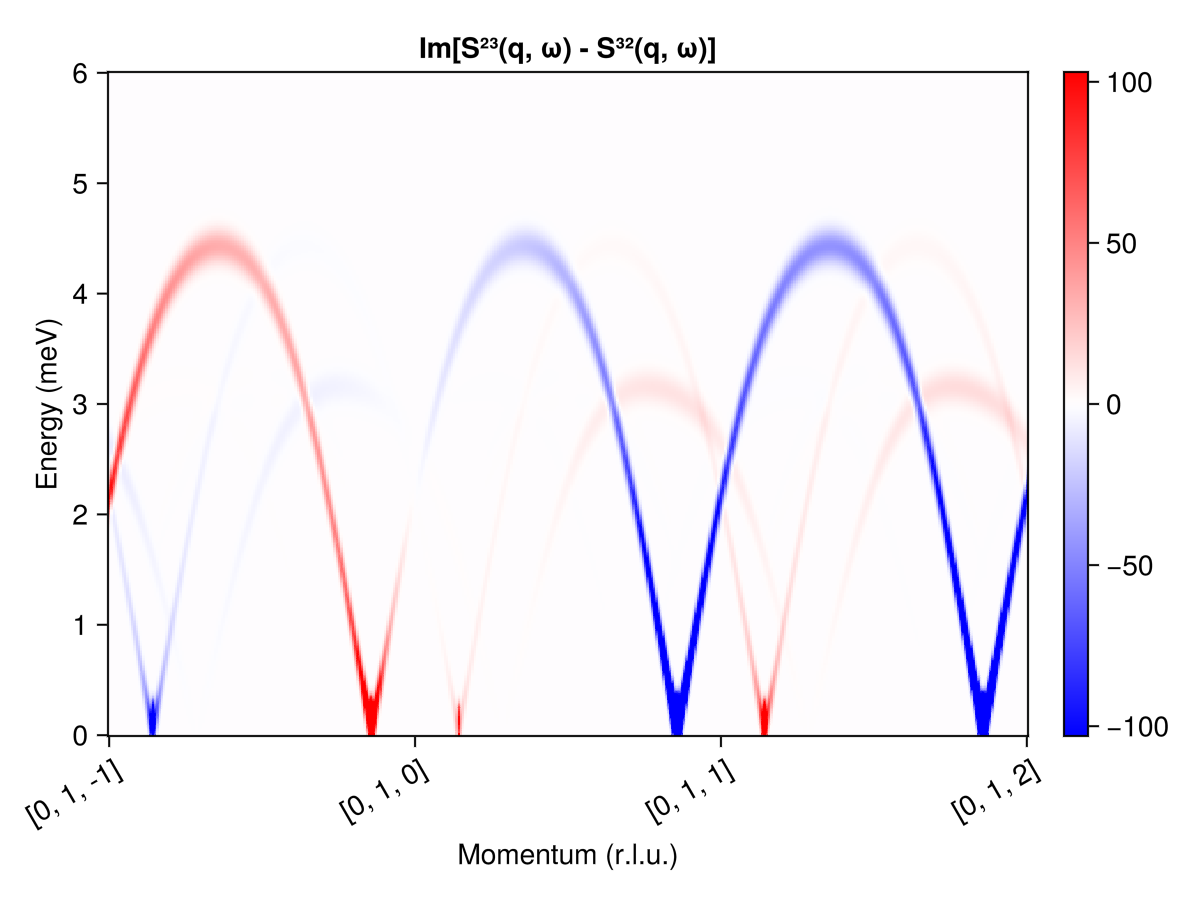
Use ssf_custom_bm to calculate the imaginary part of $\mathcal{S}^{2, 3}(𝐪, ω) - \mathcal{S}^{3, 2}(𝐪, ω)$. In polarized neutron scattering, it is conventional to express the 3×3 structure factor matrix $\mathcal{S}^{α, β}(𝐪, ω)$ in the Blume-Maleev polarization axis system. Specify the scattering plane $[0, K, L]$ via the spanning vectors $𝐮 = [0, 1, 0]$ and $𝐯 = [0, 0, 1]$.

measure = ssf_custom_bm(sys; u=[0, 1, 0], v=[0, 0, 1]) do q, ssf
    imag(ssf[2,3] - ssf[3,2])
end
swt = SpinWaveTheorySpiral(sys; measure, k, axis)
res = intensities(swt, path; energies, kernel=gaussian(fwhm=0.25))
plot_intensities(res; units, saturation=0.8, allpositive=false,
                 title="Im[S²³(q, ω) - S³²(q, ω)]")